
| 1 | 3 |
 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:013
平面上有相异10个点,每两点连线可确定的直线的条数是每三点为顶点所确定的三角形个数的![]() .若无任意四点共线,则这10个点的连线中有且只有三点共线的直线的条数为( )
.若无任意四点共线,则这10个点的连线中有且只有三点共线的直线的条数为( )
A.2条 B.3条
C.4条 D.5条
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
A.2条 B.3条
C.4条 D.5条
查看答案和解析>>
科目:高中数学 来源:山东省济宁市汶上一中2011-2012学年高二3月月考数学理科试题 题型:022
平面上有相异10个点,每两点连线可确定的直线的条数是每三点为顶点所确定的三角形个数的![]() ,若无任意四点共线,则这10个点的连线中有且只有三点共线的直线的条数为________条.
,若无任意四点共线,则这10个点的连线中有且只有三点共线的直线的条数为________条.
查看答案和解析>>
科目:高中数学 来源:2013届江西省高二下学期第二次月考理科数学试卷 题型:填空题
平面上有相异10个点,每两点连线可确定的直线的条数是每三点为顶点所确定的三角形个数的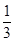 ,若无任意四点共线,则这10个点的连线中有且只有三点共线的直线的条数为__________条.
,若无任意四点共线,则这10个点的连线中有且只有三点共线的直线的条数为__________条.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com