
当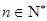 时,
时,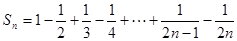
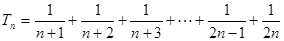
(1)求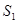 ,
,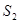 ,
,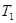 ,
,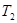 ;
;
(2)猜想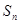 与
与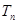 的关系,并用数学归纳法证明.
的关系,并用数学归纳法证明.
(1)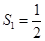 ,
,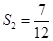
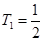
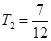
(2)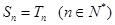 证明见解析
证明见解析
【解析】(1)分别令n=1,n=2可求出S1,S2,T1,T2.
(2)根据(I)当中的结果,猜想出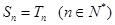 ,
,
因为是与正整数n有关的等式可以考虑采用数学归纳法证明.
再证明时一定要按两个步骤进行,缺一不可.
第一步,先验证:n=1时等式成立.
第二步,先假设n=k时,等式成立;再证明n=k+1时,等式也成立,但必须要用上n=k时,归纳假设,否则证明无效
(1)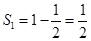 ,
,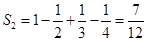
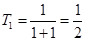
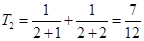 ………4分
………4分
(2)猜想: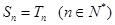 即:
即:
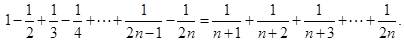 (n∈N*)6分
(n∈N*)6分
下面用数学归纳法证明
① n=1时,已证S1=T1 ………………7分
② 假设n=k时,Sk=Tk(k≥1,k∈N*),即:
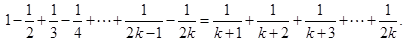 ……………9分
……………9分
则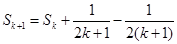
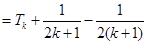 …11分
…11分

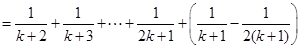
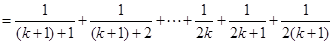
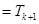
由①,②可知,对任意n∈N*,Sn=Tn都成立.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
大西洋鲑鱼每年都要逆流而上,游回产地产卵。记鲑鱼的游速为![]() ,鲑鱼的耗氧量的单位数为
,鲑鱼的耗氧量的单位数为![]() ,研究中发现
,研究中发现![]() 与
与![]() 成正比,且当
成正比,且当![]() 时,
时,![]() .
.
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)计算一条鲑鱼的游速是1.5m/s时耗氧量的单位数.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省高三第一次调研考试理科数学试卷(解析版) 题型:解答题
已知偶函数 满足:当
满足:当 时,
时, ,
,
当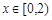 时,
时,
(1) 求当 时,
时, 的表达式;
的表达式;
(2) 试讨论:当实数 满足什么条件时,函数
满足什么条件时,函数 有4个零点,
有4个零点,
且这4个零点从小到大依次构成等差数列.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高三上学期第三次月考理科数学卷 题型:解答题
(本题满分15分)
已知偶函数 满足:当
满足:当 时,
时, ,当
,当 时,
时,
(1) 求当 时,
时, 的表达式;
的表达式;
(2) 若直线 与函数
与函数 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。
(3) 试讨论当实数 满足什么条件时,函数
满足什么条件时,函数 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。
查看答案和解析>>
科目:高中数学 来源:2012届江苏省高三数学国庆作业二(文科) 题型:解答题
已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当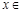
 时,
时, .
.
(1)求函数 的解析式;并判断
的解析式;并判断 在
在 上的单调性(不要求证明);
上的单调性(不要求证明);
(2)解不等式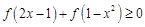 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com