练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    由原点向三次曲线引切线,切于不同于点的点

    ，再由引此曲线的切线，切于不同于的点，如此继续地作下去,……,得到点列，试回答下列问题： ⑴求； (2)求与的关系式；

    (3)若，求证:当为正偶数时, ；当为正奇数时, .

    ⑴，⑵⑶证明略


    解析:

    ⑴由  ①  得y′=3x2－6ax＋b.

    过曲线①上点的切线的方程是：

    由它过原点，有

                                           

    ⑵ 过曲线①上点的切线ln+1的方程是：

    ,由过曲线①上点，有

    ∵，以除上式，得

    以除之，得  

    (3)方法1 由(2)得

    故数列{x n－a}是以x 1－a=为首项,公比为－的等比数列,

     

    ∵，∴当为正偶数时,

    当为正奇数时,                      

    方法2

    =

    以下同解法1.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    由原点O向三次曲线y=x3-3ax2（a≠0）引切线，切点为P1（x1，y1）（O，P1两点不重合），再由P1引此曲线的切线，切于点P2（x2，y2）（P1，P2不重合），如此继续下去，得到点列：{Pn（xn，yn）}
    （1）求x1；
    （2）求xn与xn+1满足的关系式；
    （3）若a＞0，试判断xn与a的大小关系，并说明理由

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    由原点O向三次曲线y=x3-3ax2+bx（a≠0）引切线，切于不同于点O的点P1（x1，y1），再由P1引此曲线的切线，切于不同于P1的点P2（x2，y2），如此继续地作下去，…，得到点列{Pn（xn，yn）}，试回答下列问题：
    （1）求x1；
    （2）求xn与xn+1的关系；
    （3）若a＞0，求证：当n为正偶数时，xn＜a；当n为正奇数时，xn＞a．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    (2006黄冈模拟)由原点O向三次曲线引切线，切于点(O、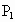两点不重合)，再由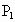引此曲线的切线，切于点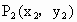(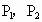不重合)，如此继续下去，得到点．

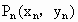    (1)求；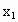

    (2)求与满足的关系式；

    (3)若a＞0，试判断与a的大小关系并说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江西省吉安市白鹭洲中学高三（上）第二次月考数学试卷（理科）（解析版） 题型：解答题

    由原点O向三次曲线y=x3-3ax2+bx （a≠0）引切线，切于不同于点O的点P1（x1，y1），再由P1引此曲线的切线，切于不同于P1的点P2（x2，y2），如此继续地作下去，…，得到点列{ P n（x n，y n）}，试回答下列问题：
    （1）求x1；
    （2）求xn与xn+1的关系；
    （3）若a＞0，求证：当n为正偶数时，xn＜a；当n为正奇数时，xn＞a．

    查看答案和解析>>

    同步练习册答案