
【题目】在数列{an}中,a3=12,a11=﹣5,且任意连续三项的和均为11,则a2017=;设Sn是数列{an}的前n项和,则使得Sn≤100成立的最大整数n= .
【答案】4;29
【解析】解:由题意可得an+an+1+an+2=11,
将n换为an+1+an+2+an+3=11,
可得an+3=an,
可得数列{an}是周期为3的数列.
a3=12,a11=﹣5,即有a2=﹣5,a1=11﹣12+5=4,
可得a2017=a3×672+1=a1=4;
当n=3k,k为自然数,时,Sn=11k;
当n=3k+1,k为自然数时,Sn=11k+4;
当n=3k+2,k为自然数时,Sn=11k+4﹣5=11k﹣1;
使得Sn≤100成立,
由11k≤100,可得k的最大值为9,此时n=27;
由11k+4≤100,可得k的最大值为8,此时n=25;
由11k﹣1≤100,可得k的最大值为9,此时n=29.
则使得Sn≤100成立的最大整数n为29.
所以答案是:4,29.
【考点精析】掌握数列的前n项和是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系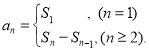 .
.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆W: ![]() ,过原点O作直线l1交椭圆W于A,B两点,P为椭圆上异于A,B的动点,连接PA,PB,设直线PA,PB的斜率分别为k1 , k2(k1 , k2≠0),过O作直线PA,PB的平行线l2 , l3 , 分别交椭圆W于C,D和E,F.
,过原点O作直线l1交椭圆W于A,B两点,P为椭圆上异于A,B的动点,连接PA,PB,设直线PA,PB的斜率分别为k1 , k2(k1 , k2≠0),过O作直线PA,PB的平行线l2 , l3 , 分别交椭圆W于C,D和E,F.
(1)若A,B分别为椭圆W的左、右顶点,是否存在点P,使∠APB=90°?说明理由.
(2)求k1k2的值;
(3)求|CD|2+|EF|2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆M的方程为x2+y2﹣8x﹣2y+16=0,若直线kx﹣y+3=0上至少存在一点,使得以该点为圆心,半径为1的圆与圆M有公共点,则k的取值范围是( )
A.(﹣∞, ![]() ]
]
B.[0,+∞)
C.[﹣ ![]() ,0]
,0]
D.(﹣∞, ![]() ]∪[0,+∞)
]∪[0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某电视台综艺节目举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( ) 
A.84,4.84
B.84,1.6
C.85,4
D.85,1.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在无穷数列{an}中,a1=p是正整数,且满足  (Ⅰ)当a3=9时,给出p的值;(结论不要求证明)
(Ⅰ)当a3=9时,给出p的值;(结论不要求证明)
(Ⅱ)设p=7,数列{an}的前n项和为Sn , 求S150;
(Ⅲ)如果存在m∈N* , 使得am=1,求出符合条件的p的所有值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和 ![]() ,其中n∈N* . (Ⅰ)求数列{an}的通项公式;
,其中n∈N* . (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设 ![]() ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(Ⅲ)若对于任意正整数n,都有 ![]() ,求实数λ的最小值.
,求实数λ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com