
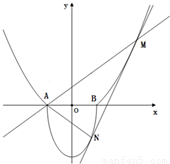
 如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线
如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线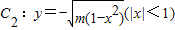 也相切于点N,记点M的横坐标为t(t>1).
也相切于点N,记点M的横坐标为t(t>1).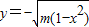 ,
, ,与已知|xN|<1矛盾;
,与已知|xN|<1矛盾;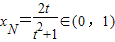 满足条件,
满足条件,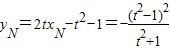 ,
,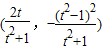 .
.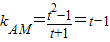 ,
, ,
,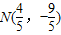 ,
,

科目:高中数学 来源: 题型:
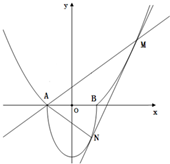 如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线C2:y=-
如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线C2:y=-| m(1-x2) |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省南昌二中高二(上)期中数学试卷(理科)(解析版) 题型:解答题
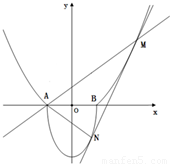 如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线
如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线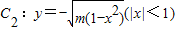 也相切于点N,记点M的横坐标为t(t>1).
也相切于点N,记点M的横坐标为t(t>1).查看答案和解析>>
科目:高中数学 来源:2009-2010学年浙江省温州市四校联考高二(下)期末数学试卷(理科)(解析版) 题型:解答题
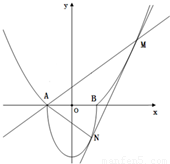 如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线
如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线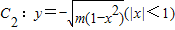 也相切于点N,记点M的横坐标为t(t>1).
也相切于点N,记点M的横坐标为t(t>1).查看答案和解析>>
科目:高中数学 来源:2009-2010学年浙江省杭州二中、学军中学、效实中学、嘉兴一中、杭州高中五校高三第二次联考数学试卷(理科)(解析版) 题型:解答题
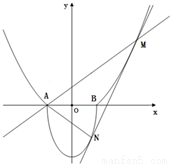 如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线
如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线 也相切于点N,记点M的横坐标为t(t>1).
也相切于点N,记点M的横坐标为t(t>1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com