分析:(I)设BD与AC交于O,则BD⊥AC,连接A
1O,以OB,OC,OA
1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,求出
与
的坐标,计算它们的数量积从而得到BD⊥AA
1(II)平面AA
1C
1C的一个法向量为n
1=(1,0,0),求出平面AA
1D的一个法向量n
2,计算两法向量的余弦值从而得到二面角D-A
1A-C的平面角的余弦值;
(III)假设在直线CC
1上存在点P,使BP∥平面DA
1C
1,设
=λ,求出平面DA
1C
1的法向量n
3,根据法向量n
3与
垂直求出λ的值,从而得到点P在C
1C的延长线上,且C
1C=CP.
解答: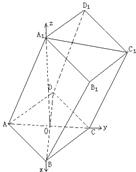
解:设BD与AC交于O,则BD⊥AC,连接A
1O,在△AA
1O中,AA
1=2,AO=1,∠A
1AO=60°,
所以A
1O
2=AA
12+AO
2-2AA
1•AOcos60°=3,
所以AO
2+A
1O
2=AA
12,所以A
1O⊥AO.
由于平面AA
1C
1C⊥平面ABCD,所以A
1O⊥平面ABCD.
以OB,OC,OA
1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则A(0,-1,0),
B(,0,0),C(0,1,0),
D(-,0,0),
A1(0,0,),
C1(0,2,)(I)由于
=(-2,0,0),=(0,1,),
•=0×(-2)+1×0+×0=0,∴BD⊥AA
1(II)由于OB⊥平面AA
1C
1C,
∴平面AA
1C
1C的一个法向量为n
1=(1,0,0)
设n
2⊥平面AA
1D,则
,
设n
2=(x,y,z),则
取
n2=(1,,-1),∴
cos<n1,n2>=所以,二面角D-A
1A-C的平面角的余弦值为
(III)假设在直线CC
1上存在点P,使BP∥平面DA
1C
1,设
=λ,P(x,y,z),则
(x,y-1,z)=λ(0,1,),从而有
P(0,1+λ,λ),=(-,1+λ,λ)设n
3⊥平面DA
1C
1,则
,又
=(0,2,0),=(,0,)设n
3=(x
3,y
3,z
3),则
,取n
3=(1,0,-1)
因为BP∥平面DA
1C
1,则
n3⊥,即n3•=--λ=0,得λ=-1
即点P在C
1C的延长线上,且C
1C=CP
点评:本题主要考查了二面角及其度量,以及平面与平面平行的判定和空间中直线与直线之间的位置关系与空间向量,考查空间想象能力、运算能力和推理论证能力,属于中档题.

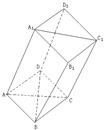 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD. 解:设BD与AC交于O,则BD⊥AC,连接A1O,在△AA1O中,AA1=2,AO=1,∠A1AO=60°,
解:设BD与AC交于O,则BD⊥AC,连接A1O,在△AA1O中,AA1=2,AO=1,∠A1AO=60°,

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.
如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.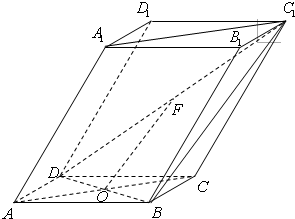 17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.
17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.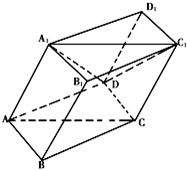 如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?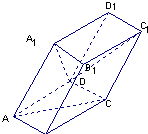 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60°
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60°