
【题目】在数学上,常用符号来表示算式,如记![]() =
=![]() ,其中
,其中![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,…,
,…,![]() 成等差数列,且
成等差数列,且![]() ,求证:
,求证:![]()
![]() ;
;
(2)若![]() ,
,![]() ,记
,记![]() ,且不等式
,且不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+![]() )(A>0,ω>0)的最小正周期为3π,则( )
)(A>0,ω>0)的最小正周期为3π,则( )
A. 函数f(x)的一个零点为![]()
B. 函数f(x)的图象关于直线x=![]() 对称
对称
C. 函数f(x)图象上的所有点向左平移![]() 个单位长度后,所得的图象关于y轴对称
个单位长度后,所得的图象关于y轴对称
D. 函数f(x)在(0,![]() )上单调递增
)上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①函数![]() 的值域是
的值域是![]() ,则函数
,则函数![]() 的值域为
的值域为![]() ;
;
②把函数![]() 图像上的每一个点的横坐标伸长到原来的4倍,然后再向右平移
图像上的每一个点的横坐标伸长到原来的4倍,然后再向右平移![]() 个单位得到的函数解析式为
个单位得到的函数解析式为![]() ;
;
③已知![]() ,则与
,则与![]() 共线的单位向量为
共线的单位向量为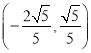 ;
;
④一条曲线![]() 和直线
和直线![]() 的公共点个数是m,则m的值不可能是1.
的公共点个数是m,则m的值不可能是1.
其中正确的有___________(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在圆心角为直角,半径为![]() 的扇形区域内进行野外生存训练.如图所示,在相距
的扇形区域内进行野外生存训练.如图所示,在相距![]() 的
的![]() ,
,![]() 两个位置分别为300,100名学生,在道路
两个位置分别为300,100名学生,在道路![]() 上设置集合地点
上设置集合地点![]() ,要求所有学生沿最短路径到
,要求所有学生沿最短路径到![]() 点集合,记所有学生进行的总路程为
点集合,记所有学生进行的总路程为![]() .
.
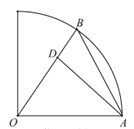
(1)设![]() ,写出
,写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)当![]() 最小时,集合地点
最小时,集合地点![]() 离点
离点![]() 多远?
多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日![]() 点的轨道运行.
点的轨道运行.![]() 点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,
点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,![]() 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
![]() .
.
设![]() ,由于
,由于![]() 的值很小,因此在近似计算中
的值很小,因此在近似计算中![]() ,则r的近似值为
,则r的近似值为
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果直线a平行于平面![]() ,则( )
,则( )
A.平面![]() 内有且只有一直线与a平行
内有且只有一直线与a平行
B.平面![]() 内有无数条直线与a平行
内有无数条直线与a平行
C.平面![]() 内不存在与a平行的直线
内不存在与a平行的直线
D.平面![]() 内的任意直线与直线a都平行
内的任意直线与直线a都平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题
①若三个平面两两相交,则它们的交线只能平行或重合;
②若a、b是异面直线,则过不在a、b上的任一点一定可以作一条直线和a、b都相交;
③正三棱锥![]() 的底面边长为a,侧棱长为b,若过SA、SB的中点作平行于侧棱SC的截面,则截面面积为
的底面边长为a,侧棱长为b,若过SA、SB的中点作平行于侧棱SC的截面,则截面面积为![]() ;
;
④过球面上任意给定两点的平面与球面相截时其截面面积最大,则这样的平面只有一个.
其中( ).
A. 只有①,②成立.
B. 只有③成立.
C. 只有④ 成立.
D. ①、②、③、④都不成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
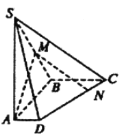
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,侧棱
是直角梯形,侧棱![]() 底面
底面![]() ,
,![]() 垂直于
垂直于![]() 和
和![]() ,
,![]() 为棱
为棱![]() 上的点,
上的点,![]() ,
,![]() .
.
(1)若![]() 为棱
为棱![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)当![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)在第(2)问条件下,设点![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求当
,求当![]() 取最大值时点
取最大值时点![]() 的位置.
的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com