
【题目】定义在R上的偶函数f(x)满足f(x+1)= ![]() ,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
A.f(sinα)>f(sinβ)
B.f(cosα)>f(cosβ)
C.f(sinα)>f(cosβ)
D.f(sinα)<f(cosβ)
【答案】C
【解析】解:∵f(x+1)= ![]() ,∴f(x+2)=f(x),f(x)是周期为2的周期函数. ∵y=f(x)是定义在R上的偶函数,∴f(﹣x)=f(x),∵f(x)在[﹣3,﹣2]上是减函数,
,∴f(x+2)=f(x),f(x)是周期为2的周期函数. ∵y=f(x)是定义在R上的偶函数,∴f(﹣x)=f(x),∵f(x)在[﹣3,﹣2]上是减函数,
∴在[2,3]上是增函数,∴在[0,1]上是增函数,∵α,β是锐角三角形的两个内角.
∴α+β>90°,α>90°﹣β,两边同取正弦得:sinα>sin(90°﹣β)=cosβ,
且sinα、cosβ都在区间[0,1]上,
∴f(sinα)>f(cosβ),
故选:C.
由条件f(x+1)= ![]() 得到f(x)是周期为2的周期函数,由f(x)是定义在R上的偶函数,在[﹣3,﹣2]上是减函数,得到f(x)在[2,3]上是增函数,在[0,1]上是增函数,再由α,β是锐角三角形的两个内角,得到α>90°﹣β,且sinα、cosβ都在区间[0,1]上,从而得到f(sinα)>f(cosβ).
得到f(x)是周期为2的周期函数,由f(x)是定义在R上的偶函数,在[﹣3,﹣2]上是减函数,得到f(x)在[2,3]上是增函数,在[0,1]上是增函数,再由α,β是锐角三角形的两个内角,得到α>90°﹣β,且sinα、cosβ都在区间[0,1]上,从而得到f(sinα)>f(cosβ).


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某港湾的平面示意图如图所示, ![]() ,
, ![]() ,
, ![]() 分别是海岸线
分别是海岸线![]() 上的三个集镇,
上的三个集镇, ![]() 位于
位于![]() 的正南方向6km处,
的正南方向6km处, ![]() 位于
位于![]() 的北偏东
的北偏东![]() 方向10km处.
方向10km处.
(Ⅰ)求集镇![]() ,
, ![]() 间的距离;
间的距离;
(Ⅱ)随着经济的发展,为缓解集镇![]() 的交通压力,拟在海岸线
的交通压力,拟在海岸线![]() 上分别修建码头
上分别修建码头![]() ,开辟水上航线.勘测时发现:以
,开辟水上航线.勘测时发现:以![]() 为圆心,3km为半径的扇形区域为浅水区,不适宜船只航行.请确定码头
为圆心,3km为半径的扇形区域为浅水区,不适宜船只航行.请确定码头![]() 的位置,使得
的位置,使得![]() 之间的直线航线最短.
之间的直线航线最短.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱![]() 中,四边形
中,四边形![]() 为梯形,
为梯形, ![]() ,且
,且![]() .过
.过![]() 三点的平面记为
三点的平面记为![]() ,
, ![]() 与
与![]() 的交点为
的交点为![]() .
.
(I)证明: ![]() 为
为![]() 的中点;
的中点;
(II)求此四棱柱被平面![]() 所分成上下两部分的体积之比.
所分成上下两部分的体积之比.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(1, ![]() )是函数f(x)=
)是函数f(x)= ![]() ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足
ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足 ![]() =
= ![]() +1(n≥2). (Ⅰ)求数列{an}的通项公式;
+1(n≥2). (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{ ![]() }的前n项和为Tn , 问使Tn>
}的前n项和为Tn , 问使Tn> ![]() 的最小正整数n是多少?
的最小正整数n是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.

(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件2件作品获奖,问这两组哪一组获奖率较高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|﹣1≤x<3},B={x|2x﹣4≤x﹣2}.
(1)求A∩(UB);
(2)若函数f(x)=lg(2x+a)的定义域为集合C,满足AC,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行购物抽奖活动,抽奖箱中放有除编号不同外,其余均相同的20个小球,这20个小球编号的茎叶图如图所示,活动规则如下:从抽奖箱中随机抽取一球,若抽取的小球编号是十位数字为l的奇数,则为一等奖,奖金100元;若抽取的小球编号是十位数字为2的奇数,则为二等奖,奖金50元;若抽取的小球是其余编号则不中奖.现某顾客有放回的抽奖两次,两次抽奖相互独立. (I)求该顾客在两次抽奖中恰有一次中奖的概率;
(Ⅱ)记该顾客两次抽奖后的奖金之和为随机变量X,求X的分布列和数学期望.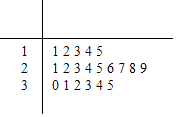
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com