
【题目】已知双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,实轴长为4,渐近线方程为
,实轴长为4,渐近线方程为![]() ,点N在圆
,点N在圆![]() 上,则
上,则![]() 的最小值为( )
的最小值为( )
A. ![]() B. 5C. 6D. 7
B. 5C. 6D. 7
【答案】B
【解析】
求得双曲线的a,b,可得双曲线方程,求得焦点坐标,运用双曲线的定义和三点共线取得最小值,连接CF2,交双曲线于M,圆于N,计算可得所求最小值.
由题意可得2a=4,即a=2,
渐近线方程为y=±![]() x,即有
x,即有![]() ,
,
即b=1,可得双曲线方程为![]() y2=1,
y2=1,
焦点为F1(![]() ,0),F2,(
,0),F2,(![]() ,0),
,0),
由双曲线的定义可得|MF1|=2a+|MF2|=4+|MF2|,
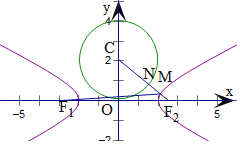
由圆x2+y2﹣4y=0可得圆心C(0,2),半径r=2,
|MN|+|MF1|=4+|MN|+|MF2|,
连接CF2,交双曲线于M,圆于N,
可得|MN|+|MF2|取得最小值,且为|CF2|![]() 3,
3,
则则|MN|+|MF1|的最小值为4+3﹣2=5.
故选:B.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
日均浓度 |
|
|
|
|
|
|
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲、乙两城市2013年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
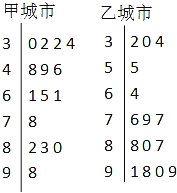
(Ⅰ)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(Ⅱ)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(Ⅲ)在乙城市15个监测数据中任取2个,设X为空气质量类别为优或良的天数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】裴波那契数列(Fibonacci sequence )又称黄金分割数列,因为数学家列昂纳多·裴波那契以兔子繁殖为例子引入,故又称为“兔子数列”,在数学上裴波那契数列被以下递推方法定义:数列![]() 满足:
满足:![]() ,
,![]() ,现从该数列的前40项中随机抽取一项,则能被3整除的概率是( )
,现从该数列的前40项中随机抽取一项,则能被3整除的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志是“连续10日,每天新增疑似病例不超过7人”.过去10日,甲、乙、丙、丁四地新增疑似病例数据信息如下:
甲地:总体平均数为3,中位数为4;
乙地:总体平均数为1,总体方差大于0;
丙地:总体平均数为2,总体方差为3;
丁地:中位数为2,众数为3;
则甲、乙、两、丁四地中,一定没有发生大规模群体感染的是( )
A.甲地B.乙地C.丙地D.丁地
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中医药,是包括汉族和少数民族医药在内的我国各民族医药的统称,是反映中华民族对生命、健康和疾病的认识,具有悠久历史传统和独特理论及技术方法的医药学体系,是中华民族的瑰宝.某科研机构研究发现,某品种中医药的药物成分甲的含量![]() (单位:克)与药物功效
(单位:克)与药物功效![]() (单位:药物单位)之间具有关系
(单位:药物单位)之间具有关系![]() .检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为
.检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为![]() 克,则估计这批中医药的药物功效的平均值为( )
克,则估计这批中医药的药物功效的平均值为( )
A.22药物单位B.20药物单位C.12药物单位D.10药物单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足:a1=![]() ,a2=
,a2=![]() ,且a1a2+a2a3+…+anan+1=na1an+1对任何的正整数n都成立,则
,且a1a2+a2a3+…+anan+1=na1an+1对任何的正整数n都成立,则![]() 的值为( )
的值为( )
A. 5032 B. 5044 C. 5048 D. 5050
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区初中学生的体质健康情况,统计了该地区8所学校学生的体质健康数据,按总分评定等级为优秀,良好,及格,不及格.良好及其以上的比例之和超过40%的学校为先进校.各等级学生人数占该校学生总人数的比例如下表:
比例 学校 等级 | 学校A | 学校B | 学校C | 学校D | 学校E | 学校F | 学校G | 学校H |
优秀 | 8% | 3% | 2% | 9% | 1% | 22% | 2% | 3% |
良好 | 37% | 50% | 23% | 30% | 45% | 46% | 37% | 35% |
及格 | 22% | 30% | 33% | 26% | 22% | 17% | 23% | 38% |
不及格 | 33% | 17% | 42% | 35% | 32% | 15% | 38% | 24% |
(1)从8所学校中随机选出一所学校,求该校为先进校的概率;
(2)从8所学校中随机选出两所学校,记这两所学校中不及格比例低于30%的学校个数为X,求X的分布列;
(3)设8所学校优秀比例的方差为S12,良好及其以下比例之和的方差为S22,比较S12与S22的大小.(只写出结果)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn,且Sn=n(n+1)(n∈N*).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)令![]() (n∈N*),求数列{cn}的前n项和Tn.
(n∈N*),求数列{cn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com