
分析 (1)用待定系数法先设函数f(x)的解析式,再由已知条件求解未知量即可,
(2)只需保证对称轴落在区间内部即可,
(3)在区间[-3,0]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,直接利用二次函数闭区间上的最值求解即可.
解答 解:(1)∵f(x)为二次函数且f(0)=f(2),
∴对称轴为x=1.
又∵f(x)最小值为1,∴可设f(x)=a(x-1)2+1 (a>0)
∵f(0)=3,∴a=2,∴f(x)=2(x-1)2+1,
即f(x)=2x2-4x+3.
(2)由条件知2a<1<a+1,∴0<a<$\frac{1}{2}$.
(3)x∈[-3,0]时,2x2-4x+3>2x+2m+1,
∴2m<2x2-6x+2,
即-3≤x≤0时:,m<x2-3x+1,
令g(x)=x2-3x+1=(x-$\frac{3}{2}$)2-$\frac{5}{4}$,(-3≤x≤0),
∴g(x)的对称轴是x=$\frac{3}{2}$,函数在[-3,0]递减,
∴g(x)min=g(0)=1,
∴m<1.
点评 本题考查函数的解析式的求法二次函数的最值,函数的恒成立条件的应用,考查分析问题解决问题的能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin15°<sin163°<cos74° | B. | sin15°<cos74°<sin163° | ||
| C. | sin163°<sin15°<cos74° | D. | cos74°<sin163°<sin15° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
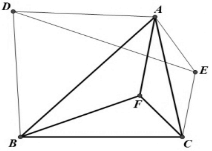 已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF.
已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若m>0,则方程x2+x-m=0有实数根”的逆否命题为:“若方程x2+x-m=0无实数根,则m≤0”. | |
| B. | 对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0. | |
| C. | 若p∧q为假命题,则p,q中至少一个为假命题. | |
| D. | “$θ=2kπ+\frac{π}{6}$”是“$sinθ=\frac{1}{2}$”的充要条件. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com