
分析 (1)讨论a的符号得出f′(x)的符号,得出f(x)的单调性,根据最大值列方程解出a;
(2)根据令g(x)=xsinx,得出g(x)的符号,估计g(x)在(0,π)的最大值与$\frac{3}{2}$的关系,结合函数图象得出答案.
解答 解:(1)f′(x)=asinx+axcosx=a(sinx+xcosx),
∵x∈[0,$\frac{π}{2}$],∴sinx+xcosx≥0,
当a=0时,f(x)=-$\frac{3}{2}$,与f(x)的最大值为$\frac{π-3}{2}$矛盾;
当a>0时,f′(x)>0,f(x)在[0,$\frac{π}{2}$]上单调递增,
∴fmax(x)=f($\frac{π}{2}$)=$\frac{aπ}{2}-\frac{3}{2}$=$\frac{π-3}{2}$,∴a=1.
当a<0时,f′(x)<0,f(x)在[0,$\frac{π}{2}$]上单调递减,
∴fmax(x)=f(0)=-$\frac{3}{2}$,与(x)的最大值为$\frac{π-3}{2}$矛盾.
综上,a=1.
(2)f(x)=xsinx-$\frac{3}{2}$,令f(x)=0得xsinx=$\frac{3}{2}$.
令g(x)=xsinx=0得x=kπ,k∈Z.
∴当0<x<π或2π<x<3π时,g(x)>0,
当π<x<2π或3π<x<4π时,g(x)<0,
且g($\frac{5π}{2}$)=$\frac{5π}{2}$,g($\frac{π}{2}$)=$\frac{π}{2}$$>\frac{3}{2}$,
作出g(x)=xsinx的大致函数图象如图所示: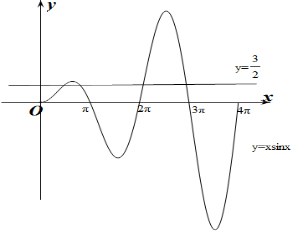
∴g(x)=$\frac{3}{2}$有4个解,即f(x)在(0,4π)上有4解.
故答案为(1)1;(2)4.
点评 本题考查了函数单调性的判断,函数零点与函数图象的关系,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 对立事件 | B. | 不可能事件 | ||
| C. | 互斥但不对立事件 | D. | 以上答案均不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
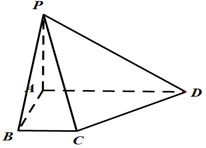 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,AD=3BC.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,AD=3BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com