【题目】一个袋子里装有7个球，其中有红球4个.白球3个.这些球除颜色外全相同.
（1）若一次从袋中取出3个球，取出的球颜色不完全相同的概率；
（2）若一次从袋中取出3个球.其中若取到红球得0分，取到白球得1分，记随机变量
为取出的三个小球得分之和，求的分布列，并求其数学期望.
科目：高中数学 来源： 题型：
【题目】商场销售某种商品的经验表明，该商品每日的销售量
(单位：千克)与销售价格
(单位：元/千克)满足关系式
，其中
，
为常数，已知销售价格为5元/千克时，每日可售出该商品11千克．
(1) 求的值；
(2) 若商品的成品为3元/千克, 试确定销售价格的值,使商场每日销售该商品所获得的利润最大
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，曲线
的参数方程为
（
， 
为参数），以坐标原点
为极点， 
轴正半轴为极轴建立极坐标系，直线
的极坐标方程为
，若直线
与曲线
相切；
（1）求曲线
的极坐标方程；
（2）在曲线
上取两点
， 
与原点
构成
，且满足
，求面积
的最大值.
【答案】（1）
；（2）
【解析】试题分析：（1）利用极坐标与直角坐标的互化公式可得直线
的直角坐标方程为
，
，消去参数
可知曲线
是圆心为
，半径为
的圆，由直线
与曲线
相切，可得： 
；则曲线C的方程为
， 再次利用极坐标与直角坐标的互化公式可得
可得曲线C的极坐标方程.
(2)由（1）不妨设M（
），
，（
），
，
，
由此可求
面积的最大值.
试题解析：（1）由题意可知直线
的直角坐标方程为
，
曲线
是圆心为
，半径为
的圆，直线
与曲线
相切，可得： 
；可知曲线C的方程为
，
所以曲线C的极坐标方程为
，
即
.
(2)由（1）不妨设M（
），，（
），
，
，
当
时， 
，
所以△MON面积的最大值为
.
【题型】解答题
【结束】
23
【题目】已知函数
的定义域为
；
（1）求实数
的取值范围；
（2）设实数
为
的最大值，若实数
， 
， 
满足
，求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
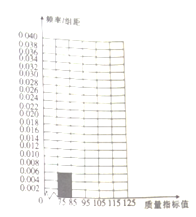
【题目】某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，现用一种新配方做试验，生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：
质量指标值 |
|
|
|
|
|
频数 | 6 | 26 | 38 | 22 | 8 |
（1）将答题卡上列出的这些数据的频率分布表填写完整，并补齐频率分布直方图；
（2）估计这种产品质量指标值的平均值（同一组中的数据用该组区间的中点值作代表）与中位数（结果精确到0.1）.
质量指标值分组 | 频数 | 频率 |
| 6 | 0.06 |
| ||
| ||
| ||
| ||
合计 | 100 | 1 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，﹣π＜φ＜0），其导函数f'（x）的部分图象如图所示，则函数f（x）的解析式为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知椭圆
上顶点为A，右焦点为F，直线
与圆
相切，其中
.
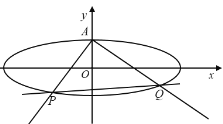
（1）求椭圆的方程；
（2）不过点A的动直线l与椭圆C相交于P，Q两点，且
，证明：动直线l过定点，并且求出该定点坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=
（c为常数），且f（1）=0．
（1）求c的值；
（2）证明函数f（x）在[0，2]上是单调递增函数；
（3）已知函数g（x）=f（ex），判断函数g（x）的奇偶性．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
