
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,点
的左、右顶点,点![]() 满足
满足![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 经过点
经过点![]() 且与
且与![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,试问:在
,试问:在![]() 轴上是否存在点
轴上是否存在点![]() ,使得直线
,使得直线 ![]() 与直线
与直线![]() 的斜率的和为定值?若存在,请求出点
的斜率的和为定值?若存在,请求出点![]() 的坐标及定值;若不存在,请说明理由.
的坐标及定值;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() ,定值为1.
,定值为1.
【解析】试题分析:
(Ⅰ)由![]() 可得
可得![]() ,再根据离心率求得
,再根据离心率求得![]() ,由此可得
,由此可得![]() ,故可得椭圆的方程.(Ⅱ)由题意可得直线
,故可得椭圆的方程.(Ⅱ)由题意可得直线![]() 的斜率存在,设出直线方程后与椭圆方程联立消元后得到一元二次方程,求出直线
的斜率存在,设出直线方程后与椭圆方程联立消元后得到一元二次方程,求出直线 ![]() 与直线
与直线![]() 的斜率,结合根与系数的关系可得
的斜率,结合根与系数的关系可得![]()
![]() ,根据此式的特点可得当
,根据此式的特点可得当![]() 时,
时,![]() 为定值.
为定值.
试题解析:
(Ⅰ)依题意得![]() 、
、![]() ,
,![]() ,
,
∴![]()
![]() ,
,
解得![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)假设存在满足条件的点![]()
![]() .
.
当直线![]() 与
与![]() 轴垂直时,它与椭圆只有一个交点,不满足题意.
轴垂直时,它与椭圆只有一个交点,不满足题意.
因此直线![]() 的斜率
的斜率![]() 存在,设直线
存在,设直线![]() 的方程为
的方程为![]() ,
,
由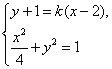 消去
消去![]() 整理得
整理得
![]() ,
,
设![]() 、
、![]() ,
,
则![]() ,
,![]() ,
,
∵![]()
![]()
![]() ,
,
∴要使对任意实数![]() ,
,![]() 为定值,则只有
为定值,则只有![]() ,
,
此时![]() .
.
故在![]() 轴上存在点
轴上存在点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 的斜率的和为定值
的斜率的和为定值![]() .
.


科目:高中数学 来源: 题型:
【题目】某食品集团生产的火腿按行业生产标准分成8个等级,等级系数![]() 依次为1,2,3,…,8,其中
依次为1,2,3,…,8,其中![]() 为标准
为标准![]() ,
, ![]() 为标准
为标准![]() .已知甲车间执行标准
.已知甲车间执行标准![]() ,乙车间执行标准
,乙车间执行标准![]() 生产该产品,且两个车间的产品都符合相应的执行标准.
生产该产品,且两个车间的产品都符合相应的执行标准.
(1)已知甲车间的等级系数![]() 的概率分布列如下表,若
的概率分布列如下表,若![]() 的数学期望E(X1)=6.4,求
的数学期望E(X1)=6.4,求![]() ,
, ![]() 的值;
的值;
X1 | 5 | 6 | 7 | 8 |
P | 0.2 |
|
|
|
(2)为了分析乙车间的等级系数![]() ,从该车间生产的火腿中随机抽取30根,相应的等级系数组成一个样本如下:3 5 3 3 8 5 5 6 3 4 6 3 4 7 5 3 4 8 5 3 8 3 4 3 4 4 7 5 6 7
,从该车间生产的火腿中随机抽取30根,相应的等级系数组成一个样本如下:3 5 3 3 8 5 5 6 3 4 6 3 4 7 5 3 4 8 5 3 8 3 4 3 4 4 7 5 6 7
用该样本的频率分布估计总体,将频率视为概率,求等级系数![]() 的概率分布列和均值;
的概率分布列和均值;
(3)从乙车间中随机抽取5根火腿,利用(2)的结果推断恰好有三根火腿能达到标准![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 与椭圆
与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,若
,若![]() ,且
,且![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)![]() ,
,![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的两点.若直线
两侧的两点.若直线![]() 过点
过点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+1(a>0,b∈R)有极值,且导函数f'(x)的极值点是f(x)的零点.(极值点是指函数取极值时对应的自变量的值)
(1)求b关于a的函数关系式,并写出定义域;
(2)证明:b2>3a;
(3)若f(x),f'(x)这两个函数的所有极值之和不小于-![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
(I)请将两家公司各一名推销员的日工资![]() (单位: 元) 分别表示为日销售件数
(单位: 元) 分别表示为日销售件数![]() 的函数关系式;
的函数关系式;
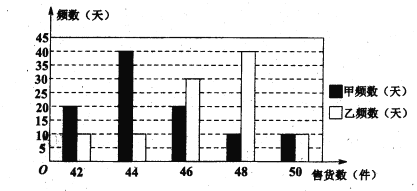
(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。若记甲公司该推销员的日工资为![]() ,乙公司该推销员的日工资为
,乙公司该推销员的日工资为![]() (单位: 元),将该频率视为概率,请回答下面问题:
(单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
【答案】(I)见解析; (Ⅱ)见解析.
【解析】分析:(I)依题意可得甲公司一名推销员的工资与销售件数的关系是一次函数的关系式,而乙公司是分段函数的关系式,由此解得;(Ⅱ)分别根据条形图求得甲、乙公司一名推销员的日工资的分布列,从而可分别求得数学期望,进而可得结论.
详解:(I)由题意得,甲公司一名推销员的日工资![]() (单位:元) 与销售件数
(单位:元) 与销售件数![]() 的关系式为:
的关系式为: ![]() .
.
乙公司一名推销员的日工资![]() (单位: 元) 与销售件数
(单位: 元) 与销售件数![]() 的关系式为:
的关系式为: 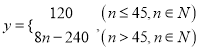
(Ⅱ)记甲公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 122 | 124 | 126 | 128 | 130 |
| 0.2 | 0.4 | 0.2 | 0.1 | 0.1 |
记乙公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 120 | 128 | 144 | 160 |
| 0.2 | 0.3 | 0.4 | 0.1 |
∴![]()
∴仅从日均收入的角度考虑,我会选择去乙公司.
点睛:求解离散型随机变量的数学期望的一般步骤为:
第一步是“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义;
第二步是“探求概率”,即利用排列组合,枚举法,概率公式,求出随机变量取每个值时的概率;
第三步是“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;
第四步是“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值
【题型】解答题
【结束】
19
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
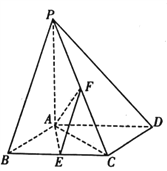
(1)证明: ![]() ;
;
(2)设![]() 为线段
为线段![]() 上的动点,若线段
上的动点,若线段![]() 长的最小值为
长的最小值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了![]() 人,将调查情况进行整理后制成下表:
人,将调查情况进行整理后制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
赞成人数 |
|
|
|
|
|
|
(![]() )完成被调查人员的频率分布直方图.
)完成被调查人员的频率分布直方图.
(![]() )若从年龄在
)若从年龄在![]() ,
,![]() 的被调查者中各随机选取
的被调查者中各随机选取![]() 人进行追踪调查,求恰有
人进行追踪调查,求恰有![]() 人不赞成的概率.
人不赞成的概率.
(![]() )在
)在![]() 在条件下,再记选中的
在条件下,再记选中的![]() 人中不赞成“车辆限行”的人数为
人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com