练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】执行下面的程序框图，若p=0.95，则输出的n=（ ）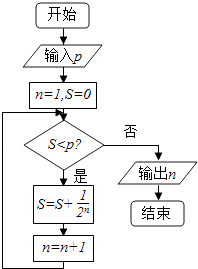

    A.4
    B.5
    C.6
    D.7

    【答案】C
    【解析】解：根据流程图所示的顺序，
    该程序的作用是判断S= + +…+ ＞0.95时，n+1的值．
    当n=2时， + =0.75＜0.95，
    当n=3时， + + =0.875＜0.95，
    当n=4时， + + + =0.9375＜0.95，
    当n=5时， + + + + =0.96875＞0.95，
    此时n+1=6．
    则输出的n=6
    故选：C
    【考点精析】认真审题，首先需要了解程序框图(程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】使函数y=xα的定义域为R且为奇函数的α的值为（ ）
    A.﹣1
    B.0
    C.
    D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=3x ， f（a+2）=27，函数g（x）=λ2ax﹣4x的定义域为[0，2]．
    （1）求a的值；
    （2）若λ=2，试判断函数g（x）在[0，2]上的单调性，并加以证明；
    （3）若函数g（x）的最大值是 ，求λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}满足a1=1， （n∈N+）．
    （1）证明：数列 是等差数列；
    （2）求数列{an}的通项公式an；
    （3）设bn=n（n+1）an ， 求数列{bn}的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知中心在坐标原点O的椭圆C经过点A（2，3），且点F（2，0）为其右焦点。

    (Ⅰ)求椭圆C的方程；

    (Ⅱ)是否存在平行于OA的直线，使得直线与椭圆C有公共点，且直线OA与的距离等于4？若存在，求出直线的方程；若不存在，请说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】徐州、苏州两地相距500千米，一辆货车从徐州匀速行驶到苏州，规定速度不得超过100千米/小时．已知货车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度v（千米/时）的平方成正比，比例系数为0.01；固定部分为a元（a＞0）．
    （1）把全程运输成本y（元）表示为速度v（千米/时）的函数，并指出这个函数的定义域；
    （2）为了使全程运输成本最小，汽车应以多大速度行驶？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥D﹣ABC中，已知△BCD是正三角形，平面ABC⊥平面BCD，AB=BC=a，AC= a，E为BC的中点，F在棱AC上，且AF=3FC．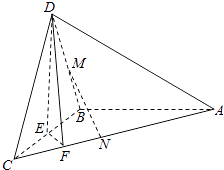

    （1）求三棱锥D﹣ABC的体积；
    （2）求证：AC⊥平面DEF；
    （3）若M为DB中点，N在棱AC上，且CN= CA，求证：MN∥平面DEF．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（13分）如图，椭圆经过点，离心率，直线l的方程为．

    （1）求椭圆C的方程；

    （2）是经过右焦点的任一弦（不经过点），设直线与直线相交于点，记、、的斜率分别为、、．问：是否存在常数，使得? 若存在，求的值； 若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数y=sin（2x﹣ ）图象向左平移 个单位，所得函数图象的一条对称轴的方程是（ ）
    A.x=
    B.x=
    C.x=
    D.x=﹣

    查看答案和解析>>

    同步练习册答案