
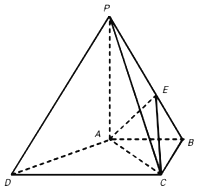
【题目】四棱锥P﹣ABCD中,AB∥CD,AB⊥BC,AB=BC=1,PA=CD=2,PA⊥平面ABCD,E在棱PB上.
(Ⅰ)求证:AC⊥PD;
(Ⅱ)若VP﹣ACE![]() ,求证:PD∥平面AEC.
,求证:PD∥平面AEC.
【答案】(Ⅰ)见解析;(Ⅱ)见解析
【解析】
(I)过![]() 作
作![]() ,判断出四边形
,判断出四边形![]() 为则方程,由此证得
为则方程,由此证得![]() ,结合
,结合![]() 证得
证得![]() 平面
平面![]() ,从而证得
,从而证得![]() .
.
(II)利用题目所给体积求得![]() 到平面
到平面![]() 的距离,连接
的距离,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,通过证明
,通过证明![]() ,证得
,证得![]() ,由此证得
,由此证得![]() 平面
平面![]() .
.
(Ⅰ)过A作AF⊥DC于F,∵AB∥CD,AB⊥BC,AB=BC=1,∴四边形ABCF为正方形,则CF=DF=AF=1,
∴∠DAC=90°,得AC⊥DA,又PA⊥底面ABCD,AC平面ABCD,∴AC⊥PA,
又PA,AD平面PAD,PA∩AD=A,∴AC⊥平面PAD,又PD平面PAD,∴AC⊥PD;
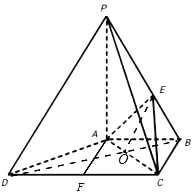
(Ⅱ)设E到平面ABCD的距离为h,则VP﹣ACE![]() ,得h
,得h![]() .
.
又PA=2,则PB:EB=PA:h=3:1.∵BC=1,CD=2,∴DB![]() ,连接DB交AC于O,连接OE,
,连接DB交AC于O,连接OE,
∵△AOB∽△COD,∴DO:OB=2:1,得DB:OB=3:1,
∴PB:EB=DB:OB,则PD∥OE.又OE平面AEC,PD平面AEC,∴PD∥平面AEC.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
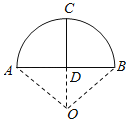
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=![]() (弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为![]() ,半径等于
,半径等于![]() 米的弧田,按照上述经验公式计算所得弧田面积约是
米的弧田,按照上述经验公式计算所得弧田面积约是 ![]()
A. ![]() 平方米 B.
平方米 B. ![]() 平方米
平方米
C. ![]() 平方米 D.
平方米 D. ![]() 平方米
平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
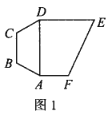
【题目】如图1,多边形ABCDEF,四边形ABCD为等腰梯形,![]() ,
,![]() ,
,![]() ,四边形ADEF为直角梯形,
,四边形ADEF为直角梯形,![]() ,
,![]() ,以AD为折痕把等腰梯形ABCD折起,使得平面
,以AD为折痕把等腰梯形ABCD折起,使得平面![]() 平面ADEF,如图2.
平面ADEF,如图2.
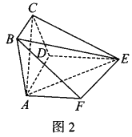
(Ⅰ)证明:![]() 平面CDE;
平面CDE;
(Ⅱ)求直线BE与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调查.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
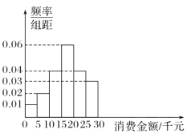
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”
列联表,并判断有多大把握认为“网购迷与性别有关系”
男 | 女 | 总计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
总计 | 100 |
附:![]() .
.
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F是拋物线C:y2=2px(p>0)的焦点,点M(x0,1)在C上,且|MF|=![]() .
.
(1)求p的值;
(2)若直线l经过点Q(3,-1)且与C交于A,B(异于M)两点,证明:直线AM与直线BM的斜率之积为常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图(如图①)、90后从事互联网行业岗位分布条形图(如图②),则下列结论中不一定正确的是( )
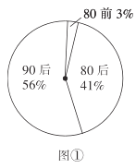
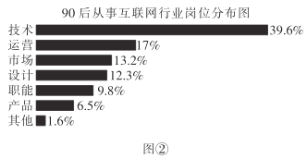
注:90后指1990年及以后出生,80后指1980~1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com