
分析 (1)通过$\overrightarrow{DM}$=$2\overrightarrow{DH}$、$\overrightarrow{NH}$$•\overrightarrow{DM}$=0可知|ND|=|NM|,等量代换可知|CN|+|ND|=4,进而可得曲线E的方程;
(2)通过记PS的中点为G,利用|PQ|=|RS|可知OG⊥PS,分直线PS的斜率存在与不存在两种情况讨论即可;
(3)通过联立直线与椭圆方程,进而结合韦达定理、在直线A′B方程中令y=0,计算即得结论.
解答  解:(1)∵$\overrightarrow{DM}$=$2\overrightarrow{DH}$,$\overrightarrow{NH}$$•\overrightarrow{DM}$=0,
解:(1)∵$\overrightarrow{DM}$=$2\overrightarrow{DH}$,$\overrightarrow{NH}$$•\overrightarrow{DM}$=0,
∴NH为DM的垂直平分线,
∴|ND|=|NM|,
又∵|CN|+|NM|=4,
∴|CN|+|ND|=4,
∴动点N的轨迹是以点C(-1,0)、D(1,0)为焦点的长轴为4的椭圆,
于是曲线E的方程为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)结论:存在直线l:y=0满足条件.
理由如下:
记PS的中点为G,则当|PQ|=|RS|时,点G为QR的中点,即OG⊥PS,
①当直线PS的斜率不存在时显然满足题意;
②假设直线PS的斜率存在,设满足题意的直线l的方程为:y=k(x-4),
并与曲线E的方程联立,消去y整理得:
(4k2+3)x2-32k2x+64k2-12=0,
设P(x1,y1),S(x2,y2),
则x1+x2=$\frac{32{k}^{2}}{4{k}^{2}+3}$,y1+y2=k(x1+x2-8)=-$\frac{24k}{4{k}^{2}+3}$,
∵OG⊥PS,
∴$\frac{\frac{{y}_{1}+{y}_{2}}{2}}{\frac{{x}_{1}+{x}_{2}}{2}}$•k=-1,即$\frac{-24k}{32{k}^{2}}$•k=-1,即$\frac{3}{4}$=1,矛盾;
综上所述,存在直线l:y=0满足条件.
(3)结论:直线A′B与x轴交于定点(4,0).
理由如下:
联立$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,整理得:(3m2+4)y2+6my-9=0,
设A(x1,y1),B(x2,y2),则A′(x1,-y1),
且y1+y2=-$\frac{6m}{3{m}^{2}+4}$,y1y2=-$\frac{9}{3{m}^{2}+4}$,
经过点A′(x1,-y1)、B(x2,y2)的直线方程为:$\frac{y+{y}_{1}}{{y}_{2}+{y}_{1}}$=$\frac{x-{x}_{1}}{{x}_{2}-{x}_{1}}$,
令y=0,则x=x1+$\frac{{x}_{2}-{x}_{1}}{{y}_{2}+{y}_{1}}$•y1=$\frac{({x}_{2}-{x}_{1}){y}_{1}+({y}_{2}+{y}_{1}){x}_{1}}{{y}_{2}+{y}_{1}}$=$\frac{{x}_{2}{y}_{1}+{x}_{1}{y}_{2}}{{y}_{1}+{y}_{2}}$,
又∵x1=my1+1,x2=my2+1,
∴当y=0时,x=$\frac{(m{y}_{2}+1){y}_{1}+(m{y}_{1}+1){y}_{2}}{{y}_{1}+{y}_{2}}$=$\frac{2m{y}_{1}{y}_{2}+({y}_{1}+{y}_{2})}{{y}_{1}+{y}_{2}}$
=$\frac{-\frac{18m}{3{m}^{2}+4}-\frac{6m}{3{m}^{2}+4}}{-\frac{6m}{3{m}^{2}+4}}$
=4,
这说明:直线A′B与x轴交于定点(4,0).
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查数形结合能力,考查分类讨论的思想,注意解题方法的积累,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 2015 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
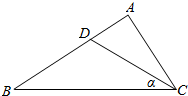 在△ABC中,BC=2AC,cosC=$\frac{3}{5}$,D是AB上的点,∠BCD=α,S△ACD:S△BCD=1:2.
在△ABC中,BC=2AC,cosC=$\frac{3}{5}$,D是AB上的点,∠BCD=α,S△ACD:S△BCD=1:2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |a|>|b| | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | a2>b2 | D. | lga>lgb |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在正方体ABCD-A1B1C1D1中,E是DD1的中点,则直线BE与平面AA1D1D所成角的正切值为( )
如图,在正方体ABCD-A1B1C1D1中,E是DD1的中点,则直线BE与平面AA1D1D所成角的正切值为( )| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $\frac{2}{5}\sqrt{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com