Question

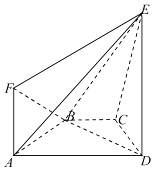
【题目】如图所示，等腰梯形ABCD的底角 A等于60°，直角梯形 ADEF所在的平面垂直于平面ABCD，∠EDA=90°，且ED=AD=2AB=2AF．

（1）证明：平面ABE⊥平面EBD；
（2）若三棱锥 A﹣BDE的外接球的体积为 ，求三棱锥 A﹣BEF的体积．

Answer 1

【答案】
（1）证明：因为平面ADEF⊥平面ABCD，

平面ADEF∩平面ABCD=AD，ED⊥AD，ED平面ADEF，

∴ED⊥平面ABCD，

∵AB平面ABCD，∴AB⊥ED，

又∵AD=2，AB=1，A=60°，∴AB⊥BD．

又BD∩ED=D，BD，ED平面EBD，

∴AB⊥平面EBD，

又AB平面ABE，所以平面ABE⊥平面EBD．

（2）解：由（1）得AD⊥DE，AB⊥BE，所以三棱锥A﹣BDE的外接球的球心为线段AE的中点．

∴ ，解得 ，

∴ ．

【解析】（1）由平面ADEF⊥平面ABCD，ED⊥AD，利用面面垂直的性质定理可得：ED⊥平面ABCD，因此AB⊥ED，又AD=2，AB=1，A=60°，故AB⊥BD，即可证明AB⊥平面EBD，于是平面ABE⊥平面EBD，（2）由（1）得AD⊥DE，AB⊥BE，可得三棱锥A﹣BDE的外接球的球心为线段AE的中点，再利用球的体积计算公式与三棱锥的体积计算公式即可得出.
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案，需要熟知一个平面过另一个平面的垂线，则这两个平面垂直．