
如图所示,设抛物线方程为x2=2py (p>0),M为直线y=-2p上任意一点,过M
 引抛物线的切线,切点分别为A,B.
引抛物线的切线,切点分别为A,B.
(1)求证:A,M,B三点的横坐标成等差数列;
(2)已知当M点的坐标为(2,-2p)时,|AB|=4![]() .求此时抛物线的方程.
.求此时抛物线的方程.
(1)证明略(2)抛物线方程为x2=2y或x2=4y.
(1)证明 由题意设A![]() ,B
,B![]() ,x1<x2,
,x1<x2,
M![]() .
.
由x2=2py得y=![]() ,则y′=
,则y′=![]() ,
,
所以kMA=![]() ,kMB=
,kMB=![]() . 2分
. 2分
因此,直线MA的方程为y+2p=![]() (x-x0),
(x-x0),
直线MB的方程为y+2p=![]() (x-x0).
(x-x0).
所以,![]() +2 p =
+2 p =![]() (x1-x0), ①
(x1-x0), ①
![]() +2 p =
+2 p =![]() (x2-x0). ② 5分
(x2-x0). ② 5分
由①、②得![]() =
=![]() ,
,
因此,x0=![]() ,即2x0=
,即2x0=![]() .
.
所以A、M、B三点的横坐标成等差数列. 8分
(2)解 由(1)知,当x0=2时,
将其代入①、②,并整理得:
x![]() -4x1-4p2=0,x
-4x1-4p2=0,x![]() -4x2-4 p 2=0,
-4x2-4 p 2=0,
所以,x1、x2是方程x2-4x-4 p 2=0的两根, 10分
因此,x1+x2=4,x1x2=-4 p 2,
又kAB= =
=![]() =
=![]() ,
,
所以kAB=![]() . 12分
. 12分
由弦长公式得
|AB|=![]()
![]()
=![]()
![]() .
.
又|AB|=4![]() ,所以p=1或p=2,
,所以p=1或p=2,
因此所求抛物线方程为x2=2y或x2=4y. 16分


 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
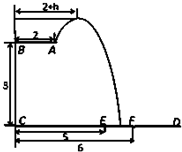 某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段,已知跳水板AB长为2m,跳水板距水面CD的高BC为3m,CE=5m,CF=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点hm(h≥1)到达距水面最大高度4m,规定:以CD为横轴,CB为纵轴建立坐标系.
某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段,已知跳水板AB长为2m,跳水板距水面CD的高BC为3m,CE=5m,CF=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点hm(h≥1)到达距水面最大高度4m,规定:以CD为横轴,CB为纵轴建立坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为
如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为| π |
| 4 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
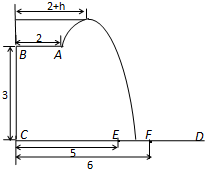 某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段.已知跳水板AB长为2m,跳水板距水面CD的高BC为3m.为安全和空中姿态优美,训练时跳水曲线应在离起跳点A处水平距hm(h≥1)时达到距水面最大高度4m.规定:以CD为横轴,BC为纵轴建立直角坐标系.
某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段.已知跳水板AB长为2m,跳水板距水面CD的高BC为3m.为安全和空中姿态优美,训练时跳水曲线应在离起跳点A处水平距hm(h≥1)时达到距水面最大高度4m.规定:以CD为横轴,BC为纵轴建立直角坐标系.查看答案和解析>>
科目:高中数学 来源:2004年高考教材全程总复习试卷·数学 题型:044
如图所示,椭圆方程为 +
+ =1(a>b>0),A,P,F分别为左顶点,上顶点,右焦点,E为x轴正方向上一点,且|
=1(a>b>0),A,P,F分别为左顶点,上顶点,右焦点,E为x轴正方向上一点,且| |,|
|,| |,|
|,| |成等比数列.又点N满足
|成等比数列.又点N满足 =
= (
( +
+ ),PF的延长线与椭圆的交点为Q,过Q与x轴平行的直线与PN的延长线交于M.
),PF的延长线与椭圆的交点为Q,过Q与x轴平行的直线与PN的延长线交于M.
(1)求证: ·
· =
= ·
· .
.
(2)若 =2
=2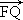 ,且|
,且| |=
|= ,求椭圆方程.
,求椭圆方程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com