
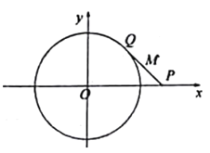
【题目】已知![]() 是
是![]() 轴上的动点(异于原点
轴上的动点(异于原点![]() ),点
),点![]() 在圆
在圆![]() 上,且
上,且![]() .设线段
.设线段![]() 的中点为
的中点为![]() ,当点
,当点![]() 移动时,记点
移动时,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)当直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,且点
,且点![]() 在第一象限.
在第一象限.
(ⅰ)求直线![]() 的斜率;
的斜率;
(ⅱ)直线![]() 平行
平行![]() ,交曲线
,交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() .线段
.线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() 、
、![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)(ⅰ)
;(2)(ⅰ)![]() ;(ⅱ)证明见解析.
;(ⅱ)证明见解析.
【解析】
(1)连接![]() ,设
,设![]() ,求出点
,求出点![]() 的坐标,然后将点
的坐标,然后将点![]() 的坐标代入圆
的坐标代入圆![]() 的方程,化简后可得出曲线
的方程,化简后可得出曲线![]() 的方程;
的方程;
(2)(i)由题意可得出![]() ,再由
,再由![]() 可判断出
可判断出![]() 为等腰直角三角形,可求出点
为等腰直角三角形,可求出点![]() 、
、![]() 的坐标,并求出点
的坐标,并求出点![]() 的坐标,由此可求出直线
的坐标,由此可求出直线![]() 的斜率;
的斜率;
(ii)设![]() ,
,![]() ,直线
,直线![]() ,将直线
,将直线![]() 的方程与曲线
的方程与曲线![]() 的方程联立,列出韦达定理,求出点
的方程联立,列出韦达定理,求出点![]() 的坐标,进而可求得直线
的坐标,进而可求得直线![]() 的方程,由此可求得点
的方程,由此可求得点![]() 、
、![]() 的坐标,再利用弦长公式化简可证得结论成立.
的坐标,再利用弦长公式化简可证得结论成立.
(1)连接![]() ,设
,设![]() ,由
,由![]() ,可得
,可得![]() ,
,
由![]() 为
为![]() 的中点,则
的中点,则![]() ,
,![]() ,
,![]() ,
,
![]() ,则
,则![]() ,
,
把![]() 代入
代入![]() ,整理得
,整理得![]() ,
,
所以曲线![]() 的方程为
的方程为![]() ;
;
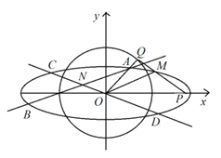
(2)(ⅰ)当直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,则
,则![]() ,
,
![]() ,则
,则![]() ,所以,
,所以,![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,
,
又点![]() 在第一象限,得
在第一象限,得![]() ,
,![]() .
.
由![]() 为
为![]() 的中点,得
的中点,得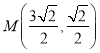 ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ;
;
(ⅱ)设![]() ,
,![]() ,直线
,直线![]() ,
,
由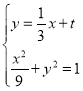 ,整理得
,整理得![]() ,
,
由韦达定理得![]() ,
,![]() .
.
所以![]() 点坐标为
点坐标为![]() ,则直线
,则直线![]() 方程为
方程为![]() .
.
由方程组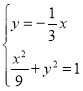 ,得
,得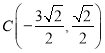 ,
,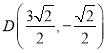 ,
,
所以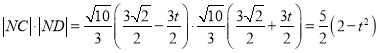 .
.
又![]()
![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为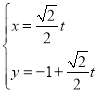 (t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为
(t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设P(0,-1),直线l与C的交点为M,N,线段MN的中点为Q,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 中,
中,![]() ,点
,点![]() 在抛物线
在抛物线![]() 上.数列
上.数列![]() 中,点
中,点![]() 在经过点
在经过点![]() ,以
,以![]() 为方向向量的直线
为方向向量的直线![]() 上.
上.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)若 ,问是否存在
,问是否存在![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)对任意的正整数![]() ,不等式
,不等式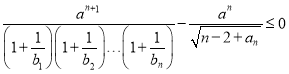 成立,求正数
成立,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为5的菱形ABCD沿对角线AC折起,顶点B移动至![]() 处,在以点B',A,C,为顶点的四面体AB'CD中,棱AC、B'D的中点分别为E、F,若AC=6,且四面体AB'CD的外接球球心落在四面体内部,则线段EF长度的取值范围为( )
处,在以点B',A,C,为顶点的四面体AB'CD中,棱AC、B'D的中点分别为E、F,若AC=6,且四面体AB'CD的外接球球心落在四面体内部,则线段EF长度的取值范围为( )
A.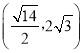 B.
B. C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
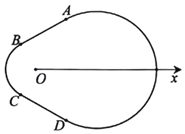
【题目】如图,有一种赛车跑道类似“梨形”曲线,由圆弧![]() 和线段AB,CD四部分组成,在极坐标系Ox中,A(2,
和线段AB,CD四部分组成,在极坐标系Ox中,A(2,![]() ),B(1,
),B(1,![]() ),C(1,
),C(1,![]() ),D(2,
),D(2,![]() ),弧
),弧![]() 所在圆的圆心分别是(0,0),(2,0),曲线M1是弧
所在圆的圆心分别是(0,0),(2,0),曲线M1是弧![]() ,曲线M2是弧
,曲线M2是弧![]() .
.
(1)分别写出M1,M2的极坐标方程:
(2)点E,F位于曲线M2上,且![]() ,求△EOF面积的取值范围.
,求△EOF面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒最近在全国蔓延,具有很强的人与人之间的传染性,该病毒在进入人体后一般有14天的潜伏期,在这14天的潜伏期内患者无任何症状,为病毒传播的最佳时间.假设每位病毒携带者在潜伏期内每天有![]() 位密切接触者,接触病毒携带者后被感染的概率为
位密切接触者,接触病毒携带者后被感染的概率为![]() ,每位密切接触者不用再接触其他病毒携带者.
,每位密切接触者不用再接触其他病毒携带者.
(1)求一位病毒携带者一天内感染的人数![]() 的均值;
的均值;
(2)若![]() ,
,![]() 时,从被感染的第一天算起,试计算某一位病毒携带者在14天潜伏期内,被他平均累计感染的人数(用数字作答);
时,从被感染的第一天算起,试计算某一位病毒携带者在14天潜伏期内,被他平均累计感染的人数(用数字作答);
(3)3月16日20时18分,由我国军事科学院军事科学研究院陈薇院士领衔的科学团队,研制重组新型冠状病毒疫苗获批进入临床状态,新疫苗的使用,可以极大减少感染新型冠状病毒的人数,为保证安全性和有效性,某科研团队抽取500支新冠疫苗,观测其中某项质量指标值,得到如下频率分布直方图:
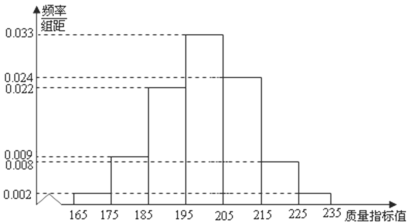
①求这500支该项质量指标值的样本平均值![]() (同一组的数据用该组区代表间的中点值)
(同一组的数据用该组区代表间的中点值)
②由直方图可以认为,新冠疫苗的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算可得这500支新冠疫苗该项指标值的样本方差
,经计算可得这500支新冠疫苗该项指标值的样本方差![]() .现有5名志愿者参与临床试验,观测得出该项指标值分别为:206,178,195,160,229,试问新冠疫苗的该项指标值是否正常,为什么?
.现有5名志愿者参与临床试验,观测得出该项指标值分别为:206,178,195,160,229,试问新冠疫苗的该项指标值是否正常,为什么?
参考数据:![]() ,若
,若![]()
![]() ,则
,则![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为提高服务质量,随机调查了60名男顾客和80名女顾客,每位顾客均对该商场的服务给出满意或不满意的评价,得到下面不完整的列联表:
满意 | 不满意 | 合计 | |
男顾客 | 50 | ||
女顾客 | 50 | ||
合计 |
(1)根据已知条件将列联表补充完整;
(2)能否有![]() 的把握认为男、女顾客对该商场服务的评价有差异?
的把握认为男、女顾客对该商场服务的评价有差异?
附: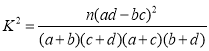
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com