
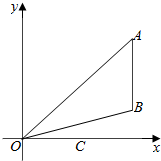
 已知O为坐标原点,向量$\overrightarrow{OA}$=(3cosx,3sinx),$\overrightarrow{OB}$=(3cosx,sinx),$\overrightarrow{OC}$=($\sqrt{3}$,0),x∈(0,$\frac{π}{2}$).
已知O为坐标原点,向量$\overrightarrow{OA}$=(3cosx,3sinx),$\overrightarrow{OB}$=(3cosx,sinx),$\overrightarrow{OC}$=($\sqrt{3}$,0),x∈(0,$\frac{π}{2}$).分析 (1)计算($\overrightarrow{OA}-\overrightarrow{OB}$)$•\overrightarrow{OC}$=0即可;
(2)由AB=BC列出方程解出.
解答 解:(1)∵$\overrightarrow{OA}-\overrightarrow{OB}$=(0,2sinx),
∴$(\overrightarrow{OA}-\overrightarrow{OB})•\overrightarrow{OC}=0×\sqrt{3}+2sinx×0=0$,
∴($\overrightarrow{OA}$-$\overrightarrow{OB}$)⊥$\overrightarrow{OC}$.
(2)若△ABC是等腰三角形,则AB=BC,
∴(2sinx)2=(3cosx-$\sqrt{3}$)2+sin2x,整理得:$2{cos^2}x-\sqrt{3}cosx=0$,
解得cosx=0,或cosx=$\frac{\sqrt{3}}{2}$,
∵x∈(0,$\frac{π}{2}$),∴cosx=$\frac{\sqrt{3}}{2}$,x=$\frac{π}{6}$.
点评 本题考查了平面向量的数量积运算及模长计算,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 80 | C. | 90 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com