
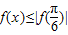 对一切x∈R恒成立,则
对一切x∈R恒成立,则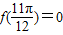 ;
;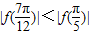 ;
;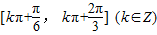 ;
;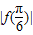 是三角函数的最大值,得到x=
是三角函数的最大值,得到x=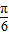 是三角函数的对称轴,将其代入整体角令整体角等于kπ+
是三角函数的对称轴,将其代入整体角令整体角等于kπ+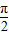 求出辅助角θ,再通过整体处理的思想研究函数的性质.
求出辅助角θ,再通过整体处理的思想研究函数的性质.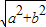 sin(2x+θ)
sin(2x+θ)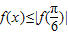
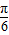 +θ=kπ+
+θ=kπ+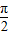
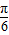
 sin(2x+kπ+
sin(2x+kπ+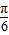 )=±
)=±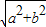 sin(2x+
sin(2x+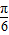 )
)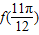 =±
=±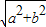 sin(2×
sin(2×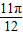 +
+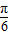 )=0,故①对
)=0,故①对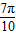 )|>|f(
)|>|f(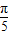 )|,故②错
)|,故②错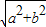 ,此时平方得b2>a2+b2这不可能,矛盾,
,此时平方得b2>a2+b2这不可能,矛盾,

科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com