练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）= ，对任意的m∈[﹣2，2]，f（mx﹣2）+f（x）＜0恒成立，则x的取值范围为_____．

    【答案】

    【解析】：由题意得，函数的定义域是R，

    且f（﹣x）=（﹣x）3+（﹣x）=﹣（x3+x）=﹣f（x），

    所以f（x）是奇函数，

    又f'（x）=3x2+1＞0，所以f（x）在R上单调递增，

    所以f（mx﹣2）+f（x）＜0可化为：f（mx﹣2）＜﹣f（x）=f（﹣x），

    由f（x）递增知：mx﹣2＜﹣x，即mx+x﹣2＜0，

    则对任意的m∈[﹣2，2]，f（mx﹣2）+f（x）＜0恒成立，

    等价于对任意的m∈[﹣2，2]，mx+x﹣2＜0恒成立，

    所以，解得﹣2＜x＜，

    即x的取值范围是，

    故答案为： ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】给出下列四个命题：
    （1函数f（x）=loga（2x﹣1）﹣1的图象过定点（1，0）；
    （2化简2 +lg5lg2+（lg2）2﹣lg2的结果为25；
    （3若loga ＜1，则a的取值范围是（1，+∞）；
    （4若2﹣x﹣2y＞lnx﹣ln（﹣y）（x＞0，y＜0），则x+y＜0．
    其中所有正确命题的序号是

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：y2=2px（p＞0）上的一点M的横坐标为3，焦点为F，且|MF|=4．直线l：y=2x﹣4与抛物线C交于A，B两点．
    （Ⅰ）求抛物线C的方程；
    （Ⅱ）若P是x轴上一点，且△PAB的面积等于9，求点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2cosxsin（x﹣ ）+ ．
    （1）求函数f（x）的对称轴方程；
    （2）若方程sin2x+2|f（x+ ）|﹣m+1=0在x∈[﹣ ， ]上有三个实数解，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列给出函数f（x）与g（x）的各组中，是同一个关于x的函数的是（ ）
    A.f（x）=x﹣1，g（x）=
    B.f（x）=2x﹣1，g（x）=2x+1
    C.f（x）=x2 ， g（x）=
    D.f（x）=1，g（x）=x0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四个命题中正确的有
    ①函数y= 的定义域是{x|x≠0}；
    ②lg =lg（x﹣2）的解集为{3}；
    ②31﹣x﹣2=0的解集为{x|x=1﹣log32}；
    ④lg（x﹣1）＜1的解集是{x|x＜11}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lg（2+x）+lg（2﹣x）．

    （1）求函数f（x）的定义域并判断函数f（x）的奇偶性；

    （2）记函数g（x）= +3x，求函数g（x）的值域；

    （3）若不等式 f（x）＞m有解，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝，AC＝3， BC＝2，P是△ABC内的一点．

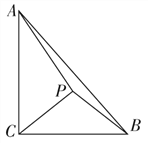
    （1）若P是等腰直角三角形PBC的直角顶点，求PA的长；

    （2）若∠BPC＝，设∠PCB＝θ，求△PBC的面积S(θ)的解析式，并求S(θ)的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数y=f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x﹣x2 ．
    （1）求x＜0时f（x）的解析式；
    （2）问是否存在正数a，b，当x∈[a，b]时，g（x）=f（x），且g（x）的值域为[ ， ]？若存在，求出所有的a，b的值，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案