
【题目】已知正项等比数列{an}满足a1 , 2a2 , a3+6成等差数列,且a42=9a1a5 .
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
【答案】解:(Ⅰ)设正项等比数列{an}的公比为q(q>0)
由 ![]() ,
,
因为q>0,所以q=3.
又因为a1,2a2,a3+6成等差数列,
所以a1+(a3+6)﹣4a2=0a1+9a1+6﹣12a1=0a1=3
所以数列{an}的通项公式为 ![]()
(Ⅱ)依题意得 ![]() ,则
,则
![]() ,
,
![]() ,
,
由﹣得 ![]() =
= ![]() ,
,
所以数列{bn}的前n项和 ![]()
【解析】(1)根据等比数列的性质“若m+n=p+q,则aman=apaq”将a42=9a1a5转化后可求出q,再根据“a、b、c成等差数列![]() 2b=a+c”列出等式,然后根据等比数列通项公式将该等式中的各项都用a1和q表示,可求出a1;(2)利用错位相减法即可求解.
2b=a+c”列出等式,然后根据等比数列通项公式将该等式中的各项都用a1和q表示,可求出a1;(2)利用错位相减法即可求解.
【考点精析】掌握等比数列的通项公式(及其变式)和数列的前n项和是解答本题的根本,需要知道通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系 .
.


科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”海选,规定:成绩大于或等于90分的具有参赛资格.某校有800名学生参加了海选,所有学生的成绩均在区间[30,150]内,其频率分布直方图如图:
(Ⅰ)求获得参赛资格的人数;
(Ⅱ)若大赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛.已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为 ![]() ,求甲在初赛中答题个数X的分布列及数学期望E(X)
,求甲在初赛中答题个数X的分布列及数学期望E(X)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法正确的是( )
①函数f(x)的定义域是R,则“x∈R,f(x+1)>f(x)”是“函数f(x)为增函数”的充要条件;
②命题“ ![]() ”的否定是“
”的否定是“ ![]() ”;
”;
③命题“若x=2,则x2﹣3x+2=0”的逆否命题是真命题;
④p:在△ABC中,若cos2A=cos2B,则A=B;q:y=sinx在第一象限是增函数,则p∧q为真命题.
A.①②③④
B.②③
C.③④
D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ,g(x)=ax+b.
,g(x)=ax+b.
(1)若函数h(x)=f(x)﹣g(x)在(0,+∞)上单调递增,求实数a的取值范围;
(2)若直线g(x)=ax+b是函数f(x)=lnx﹣ ![]() 图象的切线,求a+b的最小值;
图象的切线,求a+b的最小值;
(3)当b=0时,若f(x)与g(x)的图象有两个交点A(x1 , y1),B(x2 , y2),求证:x1x2>2e2 .
(取e为2.8,取ln2为0.7,取 ![]() 为1.4)
为1.4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求证: ![]() ;
;
(3)判断曲线y=f(x)是否位于x轴下方,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( ) 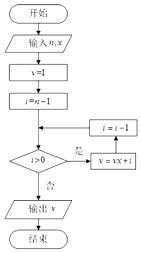
A.5
B.12
C.25
D.50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com