
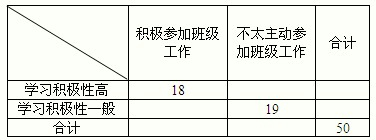
某主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示
|
|
积极参加班级工作 |
不太主动参加班级工作 |
|
学习积极性高 |
18 |
7 |
|
学习积极性一般 |
6 |
19 |
(I)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(II)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由
附:
|
P( |
0.050 |
0.010 |
0.001 |
|
|
k |
3.841 |
6.635 |
10.828 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 12 |
| 25 |
| P(K2≥ko) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:2010年湖北省秋季高二期末考试数学理卷 题型:解答题
(此题平行班做)(本小题满分12分)
某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:


(Ⅰ)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是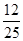 ,请完成上面的
,请完成上面的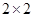 列联表;
列联表;
|
|
|
|
|
|
|
|
|
|
(Ⅱ)在(1)的条件下,试运用独立性检验的思想方法分析:在犯错误概率不超过0.1%的情况下判断学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(此题平行班做)(本小题满分12分)
某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:

(Ⅰ)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是![]() ,请完成上面的
,请完成上面的![]() 列联表;
列联表;
|
|
|
|
|
|
|
|
|
|
(Ⅱ)在(1)的条件下,试运用独立性检验的思想方法分析:在犯错误概率不超过0.1%的情况下判断学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省随州市曾都一中高二(上)12月月考数学试卷(解析版) 题型:解答题

 ,请完成上面的2×2列联表;
,请完成上面的2×2列联表;| P(K2≥ko) | 0.010 | 0.005 | 0.001 |
| k | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com