
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,且
,且![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求椭圆的离心率;
(Ⅱ)过点![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,
两点,![]() 都在
都在![]() 轴上方,并且
轴上方,并且![]() 在
在![]() 之间,且
之间,且![]() 到直线
到直线![]() 的距离是
的距离是![]() 到直线
到直线![]() 距离的
距离的![]() 倍.
倍.
①记![]() 的面积分别为
的面积分别为![]() ,求
,求![]() ;
;
②若原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求椭圆方程.
,求椭圆方程.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
试题本题以直线与椭圆的位置关系为背景.第(1)小题设计为求椭圆的离心率,只需利用条件![]() 是
是![]() 的中点,可得
的中点,可得![]() ,从而得
,从而得![]() .第(2)小题中第①题求
.第(2)小题中第①题求![]() ,需要用等积法进行转化,即
,需要用等积法进行转化,即![]() .第②题求椭圆方程,设直线
.第②题求椭圆方程,设直线![]() 方程为
方程为![]() .注意到
.注意到![]() ,和原点
,和原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]() ,从而可以确定
,从而可以确定![]() ,
,![]() ,
,![]() 的值.
的值.
试题解析:(1)因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,即
,即![]() ,又
,又![]() 、
、![]() ,
,
所以![]() ,所以
,所以![]() ;
;
(2)①解法一:过![]() 作直线
作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,依题意,
,依题意,![]() ,
,
又![]() ,故
,故![]() ,故
,故![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() 是
是![]() 中点,∴
中点,∴![]() ,∴
,∴![]() ;
;
解法二:∵![]() ,∴
,∴![]() ,椭圆方程为
,椭圆方程为![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,即有
上,即有![]() ,
,
![]()
![]()
同理![]() ,
,
又![]() ,故
,故![]() 得
得![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() 是
是![]() 中点,∴
中点,∴![]() ,∴
,∴![]() ;
;
②解法一:设![]() ,则椭圆方程为
,则椭圆方程为![]() ,
,
由①知![]() 是
是![]() 的中点,不妨设
的中点,不妨设![]() ,则
,则![]() ,
,
又![]() 都在椭圆上,即有
都在椭圆上,即有![]()
 即
即![]()

两式相减得:![]() ,解得
,解得![]() ,
,
可得![]() ,故直线
,故直线![]() 的斜率为
的斜率为 ,
,
直线![]() 的方程为
的方程为![]() ,即
,即![]()
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
依题意![]() ,解得
,解得![]() ,故椭圆方程为
,故椭圆方程为![]() .
.
解法二:设![]() ,则椭圆方程为
,则椭圆方程为![]() ,
,
由①知![]() 是
是![]() 的中点,故
的中点,故![]() ,
,
直线![]() 的斜率显然存在,不妨设为
的斜率显然存在,不妨设为![]() ,故其方程为
,故其方程为![]() ,与椭圆联立,并消去
,与椭圆联立,并消去![]() 得:
得:![]() ,整理得:
,整理得:![]() ,(*)
,(*)
设![]() ,
,![]() ,依题意:
,依题意:![]()
 ]
]
由![]()
 解得:
解得:![]()

所以![]() ,解之得:
,解之得:![]() ,即
,即![]() .
.
直线![]() 的方程为
的方程为![]() ,即
,即![]()
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
依题意![]() ,解得
,解得![]() ,故椭圆方程为
,故椭圆方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】点外卖现已成为上班族解决午餐问题的一种流行趋势.某配餐店为扩大品牌影响力,决定对新顾客实行让利促销,规定:凡点餐的新顾客均可获赠10元或者16元代金券一张,中奖率分别为![]() 和
和![]() ,每人限点一餐,且100%中奖.现有A公司甲、乙、丙、丁四位员工决定点餐试吃.
,每人限点一餐,且100%中奖.现有A公司甲、乙、丙、丁四位员工决定点餐试吃.
(Ⅰ) 求这四人中至多一人抽到16元代金券的概率;
(Ⅱ) 这四人中抽到10元、16元代金券的人数分别用![]() 、
、![]() 表示,记
表示,记![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“五一”期间,甲乙两个商场分别开展促销活动.
(Ⅰ)甲商场的规则是:凡购物满100元,可抽奖一次,从装有大小、形状相同的4个白球、4个黑球的袋中摸出4个球,中奖情况如下表:
摸出的结果 | 获得奖金(单位:元) |
4个白球或4个黑球 | 200 |
3个白球1个黑球或3个黑球1个白球 | 20 |
2个黑球2个白球 | 10 |
记![]() 为抽奖一次获得的奖金,求
为抽奖一次获得的奖金,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)乙商场的规则是:凡购物满100元,可抽奖10次.其中,第![]() 次抽奖方法是:从编号为
次抽奖方法是:从编号为![]() 的袋中(装有大小、形状相同的
的袋中(装有大小、形状相同的![]() 个白球和
个白球和![]() 个黑球)摸出
个黑球)摸出![]() 个球,若该次摸出的
个球,若该次摸出的![]() 个球颜色都相同,则可获得奖金
个球颜色都相同,则可获得奖金![]() 元;记第
元;记第![]() 次获奖概率
次获奖概率![]() .设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
.设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
①求证:![]() ;
;
②若某顾客购买120元的商品,不考虑其它因素,从获得奖金的期望分析,他应该选择哪一家商场?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】茎叶图记录了甲,乙两组各四名同学单位时间内引体向上的次数,乙组记录中有一个数据模糊,无法确认,在图中以X表示.
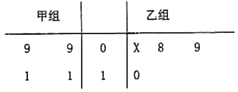
(1)如果X=8,求乙组同学单位时间内引体向上次数的平均数和方差;
(2)如果X=9,分别从甲,乙两组中随机选取一名同学,求这两名同学单位时间内引体向上次数和为19的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛.经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得10分,答错得0分.假设甲队中每人答对的概率均为![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为![]() ,
,![]() ,
,![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用![]() 表示乙队的总得分.
表示乙队的总得分.
(Ⅰ)求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)求甲、乙两队总得分之和等于30分且甲队获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:
①“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
②“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
③若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
④对于命题![]() :
:![]() ,
,![]() ,则
,则![]() 为:
为:![]() ,
,![]()
其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com