
(1)求动点M的轨迹;
(2)若动点M的轨迹在x轴上方的部分与圆心在C(a+4,0),半径为4的圆相交于两点S、T,求证:C落在以S、T为焦点过F的椭圆上.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:2010-2011学年四川省南充市高三适应性考试数学理卷 题型:选择题
已知三点A(2,3)、B(-1,-1),C(6,k),其中k为常数,若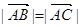 ,则向量
,则向量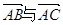 的夹角为(
)
的夹角为(
)
A.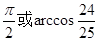 B.
B.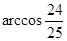
C. D.
D.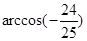
查看答案和解析>>
科目:高中数学 来源:2011年四川省南充市高考数学零诊试卷(理科)(解析版) 题型:选择题
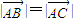 ,则
,则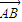 与
与 的夹角为( )
的夹角为( )
 或
或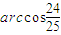

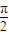 或
或
查看答案和解析>>
科目:高中数学 来源:2006年重庆市高考数学试卷(文科)(解析版) 题型:选择题
 ,则
,则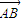 与
与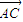 的夹角为( )
的夹角为( )
 或
或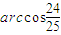

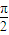 或
或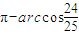
查看答案和解析>>
科目:高中数学 来源:2011届四川省南充市高三适应性考试数学理卷 题型:单选题
已知三点A(2,3)、B(-1,-1),C(6,k),其中k为常数,若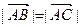 ,则向量
,则向量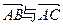 的夹角为( )
的夹角为( )
A.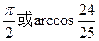 | B. |
C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com