练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本题满分12分）
    （Ⅰ）计算；
    （Ⅱ）求函数的零点.

    （Ⅰ）原式
    （Ⅱ）函数的零点是0.

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    (本大题满分13分)
    已知函数在处取得极值
    （1）求b与a的关系；
    （2）设函数，如果在区间(0,1)上存在极小值，求实数a的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本小题满分16分，每小题8分)
    求下列函数的值域：(1) ；(2) ，．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）已知定义在区间（－1，1）上的函数为奇函数。且.（1）求实数的值。
    （2）求证：函数（－1，1）上是增函数。
    （3）解关于。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）已知实数满足方程.
    （1）求的最大值和最小值；
    （2）求的最大值与最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分） 某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其注意力指数与听课时间之间的关系满足如图所示的曲线．当时，曲线是二次函数图象的一部分，当式，曲线是函数(且)图象的一部分．根据专家研究，当注意力指数大于等于80时听课效果最佳．
    (1) 试求的函数关系式；
    (2) 老师在什么时段内安排核心内容能使得学生听课效果最佳？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数在区间[0，1]上单调递增，在区间[1，2]上单调递减。（1）求实数的值.（2）设，关于的方程的解集恰有3个元素，求实数的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数
    （1）求函数的最小值和最小正周期；
    （2）设△的内角对边分别为，且，若与共线，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为了研究某种药物，用小白鼠进行试验，发现药物在血液内的浓度与时间的关系因使用方式的不同而不同。若使用注射方式给药，则在注射后的3小时内，药物在白鼠血液内的浓度与时间t满足关系式：，若使用口服方式给药，则药物在白鼠血液内的浓度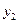与时间t满足关系式：现对小白鼠同时进行注射和口服该种药物，且注射药物和口服药物的吸收与代谢互不干扰。
    （1）若a=1，求3小时内，该小白鼠何时血液中药物的浓度最高，并求出最大值？
    （2）若使小白鼠在用药后3小时内血液中的药物浓度不低于4，求正数a的取值范围。

    查看答案和解析>>

    同步练习册答案