
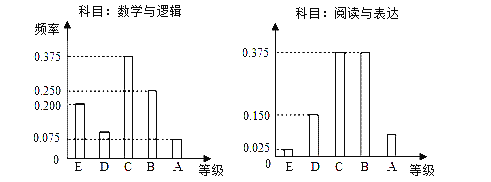
����Ŀ����ij��ѧ�������������У�����ѡ������־��Ŀ���ȫ���μ��ˡ���ѧ�������͡��Ķ�����������Ŀ�Ŀ��ԣ��ɼ���ΪA��B��C��D��E����ȼ���ij�������������ƿ��Գɼ�������ͳ������ͼ��ʾ�����С���ѧ��������Ŀ�ijɼ��ȼ�ΪB�Ŀ�����10�ˣ�
��1����ÿ��������С��Ķ�������Ŀ�гɼ��ȼ�ΪA��������
��2����֪�μӱ��������ԵĿ����У�ǡ��2�˵����Ƴɼ��ȼ���ΪA��������һ�Ƴɼ��ȼ�ΪA�Ŀ����У������ȡ2�˽��з�̸������2�˵����Ƴɼ��ȼ���ΪA�ĸ��ʣ�
���𰸡���1��3 (2) ![]()
�������������������1���������⣬����������������㿼�����Ķ�������Ŀ�гɼ��ȼ�ΪA���������ɣ���2���г����л����¼�����������ҳ�����������������ɣ�
���������(1)�ߡ���ѧ��������Ŀ�гɼ��ȼ�ΪB�Ŀ�����10�ˣ�
��ÿ�����10��0.25=40���ˣ���
��ÿ��������С��Ķ�������Ŀ�гɼ��ȼ�ΪA������Ϊ
40����1-0.375-0.375-0.15-0.025��=40��0.075=3��
��2�������ƿ����У�����6��A����ǡ��2�˵����Ƴɼ��ȼ���ΪA��
���2��ֻ��һ����Ŀ�ɼ��ȼ�ΪA��
����4��Ϊ�ס��ҡ������������мס��������Ƴɼ��ȼ�����A��ͬѧ��
��������һ�Ƴɼ��ȼ�ΪA�Ŀ����У������ȡ2�˽��з�̸��
�����¼��ռ�Ϊ![]()
![]() ��һ����6�������¼���
��һ����6�������¼���
�衰�����ȡ2�˽��з�̸����2�˵����Ƴɼ��ȼ���ΪA��Ϊ�¼�M��
���¼�M�а����Ļ����¼���1����Ϊ���ף��ң�����P(M)=![]() .
.


 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������R�ϵ��溯��f��x������x��0ʱ��f��x��=2�����溯��f��x����ֵ���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и��⣺
��1�����㣺 ![]() ��
��
��2������lg20+log10025��
��3������ ![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������R�ϵĺ���f��x����f��0����0��f��1��=2����x��0��f��x����1���Ҷ�����a��b��R����f��a+b��=f��a��f��b����
��1����֤��������x��R������f��x����0��
��2���ж�f��x����R�ϵĵ����ԣ����ö���֤����
��3����ʽf��3��2x����4�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=x2+2ax��a��1��x��[0��2]��aΪ������
��1����f��x������Сֵg��a���Ľ���ʽ��
��2���ڣ�1���У��Ƿ������С������m��ʹ��g��a����m��0��������a��R�������������ڣ����m��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ijСѧ�����ȡ100��ͬѧ�������ǵ����ߣ���λ�����ף����ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ������Ҫ��������[ 120 , 130����[130 ��140) , [140 , 150]�����ڵ�ѧ���У��÷ֲ�����ķ���ѡȡ18�˲μ�һ�������������[140 ��150]�ڵ�ѧ����ѡȡ������ӦΪ 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={x|1��x��5}������B={ ![]() ��0}��
��0}��
��1����A��B��
��2��������C={x|a+1��x��4a��3}����C��A=A����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
�� ![]() ��Ϊ�溯�������������Գ����ľ���Ϊ
��Ϊ�溯�������������Գ����ľ���Ϊ![]() .
.
��1����![]() ʱ����
ʱ����![]() �ĵ����ݼ����䣻
�ĵ����ݼ����䣻
��2��������![]() ��ͼ����
��ͼ����![]() �᷽������ƽ��
�᷽������ƽ��![]() ����λ���ȣ��ٰѺ��������̵�ԭ����
����λ���ȣ��ٰѺ��������̵�ԭ����![]() �������겻�䣩���õ�����
�������겻�䣩���õ�����![]() ��ͼ��.��
��ͼ��.��![]() ʱ������
ʱ������![]() ��ֵ��.
��ֵ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ƿ����μ������������ԣ���7������(4��������3���Ŀ���)���Żص�������ȡ3������.
(1)��ÿ����ڵ�һ�γ鵽������������£��ڶ��κ͵����ξ��鵽������ĸ��ʣ�
(2)�ÿ������������ĸ��ʾ�Ϊ![]() ����ÿ���Ե�10�֣��������֣��ָ����鵽3�������⣬���������ܷ�
����ÿ���Ե�10�֣��������֣��ָ����鵽3�������⣬���������ܷ�![]() �ķֲ�������ѧ����
�ķֲ�������ѧ����![]() .
.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com