
【题目】如图,直线l:y=x+b与抛物线C:x2=4y相切于点A. 
(1)求实数b的值;
(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程.
【答案】
(1)解:由 ![]() 得x2﹣4x﹣4b=0,①
得x2﹣4x﹣4b=0,①
因为直线l与抛物线C相切,所以△=(﹣4)2﹣4×(﹣4b)=0,
解得b=﹣1
(2)解:由(1)可知b=﹣1,故方程①即为x2﹣4x+4=0,解得x=2,代入x2=4y,得y=1.
故点A(2,1),
因为圆A与抛物线C的准线相切,
所以圆A的半径r等于圆心A到抛物线的准线y=﹣1的距离,即r=|1﹣(﹣1)|=2,
所以圆A的方程为(x﹣2)2+(y﹣1)2=4.

【解析】(1)由题意,联立方程组,根据判别式从而求实数b的值;(2)求出点A的坐标,因为圆A与抛物线C的准线相切,所以圆A的半径r等于圆心A到抛物线的准线y=﹣1的距离,问题得以解决.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
【题目】高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.
(1)求x和y的值;
(2)计算甲组7位学生成绩的方差S2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() (其中e为自然对数的底数),
(其中e为自然对数的底数), ![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)设![]() ,.已知直线
,.已知直线![]() 是曲线
是曲线![]() 的切线,且函数
的切线,且函数![]() 上是增函数.
上是增函数.
(i)求实数![]() 的值;
的值;
(ii)求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,且直线
,且直线![]() 是函数
是函数![]() 的一条切线.
的一条切线.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅲ)已知方程![]() 有两个根
有两个根![]() (
(![]() ),若
),若![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电影院共有1000个座位,票价不分等次,根据影院的经营经验,当每张票价不超过10元时,票可全售出;当每张票价高于10元时,每提高1元,将有30张票不能售出,为了获得更好的收益,需给影院定一个合适的票价,需符合的基本条件是:①为了方便找零和算账,票价定为1元的整数倍;②电影院放一场电影的成本费用支出为5750元,票房的收入必须高于成本支出,用x(元)表示每张票价,用y(元)表示该影院放映一场的净收入(除去成本费用支出后的收入)问:
(1)把y表示为x的函数,并求其定义域;
(2)试问在符合基本条件的前提下,票价定为多少时,放映一场的净收人最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
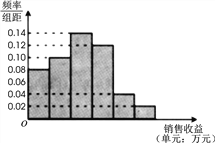
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知an=logn+1(n+2)(n∈N+),观察下列运算:a1a2=log23log34= ![]() =2;a1a2a3a4a5a6=log23log34…log67lg78=
=2;a1a2a3a4a5a6=log23log34…log67lg78= ![]() =3;….定义使a1a2a3…ak为整数的k(k∈N+)叫做希望数,则在区间[1,2016]内所有希望数的和为( )
=3;….定义使a1a2a3…ak为整数的k(k∈N+)叫做希望数,则在区间[1,2016]内所有希望数的和为( )
A.1004
B.2026
C.4072
D.22016﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com