练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    方程x2-（k+2）x+1-3k=0有两个不等实根x1，x2，且0＜x1＜1＜x2＜2，则实数k的取值范围为________．

    （0，）
    分析：构造函数f（x）=x2-（k+2）x+1-3k，根据方程x2-（k+2）x+1-3k=0有两个不等实根x1，x2，且0＜x1＜1＜x2＜2，建立不等式，从而求得实数k的取值范围．
    解答：构造函数f（x）=x2-（k+2）x+1-3k
    ∵方程x2-（k+2）x+1-3k=0有两个不等实根x1，x2，且0＜x1＜1＜x2＜2，
    ∴
    ∴
    ∴
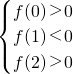
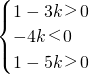
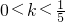
    ∴实数k的取值范围为（0，）
    故答案为：（0，）
    点评：本题重点考查方程根的分布，考查解不等式，解题的关键是构造函数，用函数思想研究方程根的问题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若方程x2+（k+2）x-k=0的两实根均在区间（-1，1）内，求k的取值范围
    [-4+2
    		3
    ，-
    1
    2
    )
    [-4+2
    		3
    ，-
    1
    2
    )
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若方程x2+（k-2）x+2k-1=0的两根中，一根在0和1之间，另一根在1和2之间，则实数k的取值范围是
    (
    1
    2
    ，
    2
    3
    )
    (
    1
    2
    ，
    2
    3
    )
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若α，β是关于x的方程x2-（k-2）x+k2+3k+5=0的两根，求α2+β2的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若α、β是关于x的方程x2-（k-2）x+k2+3k+5=0（k∈R）的两个实根，则α2+β2的最大值等于（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知方程x2+（k-2）x+k2+1=0，求使方程有两个大于1的根的充要条件．

    查看答案和解析>>

    同步练习册答案