【题目】函数f（x）的图象如图所示，曲线BCD为抛物线的一部分．
（Ⅰ）求f（x）解析式；
（Ⅱ）若f（x）=1，求x的值；
【答案】(1) 
（2）
或
.
【解析】
（1）当﹣1≤x≤0时图形为直线，根据两点坐标可求出解析式；当0＜x≤3时，函数图象为抛物线，设函数解析式为y=a（x﹣1）（x﹣3），带入坐标点可求出抛物线方程；
（2）函数f（x）图形与直线y=1的交点横坐标即为所求x的值.
（1）当-1≤x≤0时，函数图象为直线且过点（-1，0）（0，3），直线斜率为k=3，
所以y=3x+3；
当0＜x≤3时，函数图象为抛物线，设函数解析式为y=a（x-1）（x-3），
当x=0时，y=3a=3，解得a=1，所以y=（x-1）（x-3）=x2-4x+3，
所以
．
（2）当x∈[-1，0]，令3x+3=1，解得
；
当x∈（0，3]，令x2-4x+3=1，解得
，
因为0＜x≤3，所以x=
，
所以
或；
金钥匙试卷系列答案科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝ax－1(a>0且a≠1)．
(1)若函数y＝f(x)的图象经过点P(3,4)，求a的值；
(2)当a变化时，比较f(lg
)与f(－2.1)的大小，并写出比较过程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设顶点在原点，焦点在
轴上的拋物线过点
，过
作抛物线的动弦
， 
，并设它们的斜率分别为
， 
.
(Ⅰ)求拋物线的方程；
(Ⅱ)若
，求证：直线
的斜率为定值，并求出其值；
（III）若
，求证：直线
恒过定点，并求出其坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，某几何体的三视图都是直角三角形，则该几何体的体积等于__________．
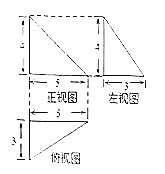
【答案】10
【解析】几何体为三棱锥，（高为4，底面为直角三角形），体积为
点睛:空间几何体体积问题的常见类型及解题策略
(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体，则可直接利用公式进行求解．
(2)若所给定的几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法进行求解．
(3)若以三视图的形式给出几何体，则应先根据三视图得到几何体的直观图，然后根据条件求解．
【题型】填空题
【结束】
15
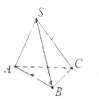
【题目】如图：在三棱锥
中，已知底面
是以
为斜边的等腰直角三角形，且侧棱长
，则三棱锥
的外接球的表面积等于__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数列{an}满足a1=1，nan+1=（n+1）an+n（n+1），n∈N* ．
（1）证明：数列{ 
}是等差数列；
（2）设bn=3n 
，求数列{bn}的前n项和Sn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义非零向量
的“相伴函数”为
（
），向量称为函数的“相伴向量”（其中
为坐标原点），记平面内所有向量的“相伴函数”构成的集合为
.
（1）已知
（
），求证：
，并求函数
的“相伴向量”模的取值范围；
（2）已知点（
）满足
，向量
的 “相伴函数”
在
处取得最大值，当点
运动时，求
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
