
【题目】某中学为调查该校学生每周参加社会实践活动的情况,随机收集了若干名学生每周参加社会实践活动的时间(单位:小时),将样本数据绘制如图所示的频率分布直方图,且在[0,2)内的学生有1人.
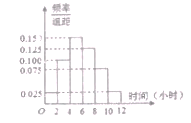
(1)求样本容量![]() ,并根据频率分布直方图估计该校学生每周参加社会实践活动时间的平均值;
,并根据频率分布直方图估计该校学生每周参加社会实践活动时间的平均值;
(2)将每周参加社会实践活动时间在[4,12]内定义为“经常参加社会实践”,参加活动时间在[0,4)内定义为“不经常参加社会实践”.已知样本中所有学生都参加了青少年科技创新大赛,有13人成绩等级为“优秀”,其余成绩为“一般”,其中成绩优秀的13人种“经常参加社会实践活动”的有12人.请将2×2列联表补充完整,并判断能否在犯错误的概率不超过0.05的前提下认为青少年科技创新大赛成绩“优秀”与经常参加社会实践活动有关;
(3)在(2)的条件下,如果从样本中“不经常参加社会实践”的学生中随机选取两人参加学校的科技创新班,求其中恰好一人成绩优秀的概率.
参考公式和数据:
![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【答案】(1)![]() ,5.8小时;(2)见解析;(3)
,5.8小时;(2)见解析;(3)![]()
【解析】分析:(1)先根据条件求得样本容量![]() ,然后再根据频率分布直方图中平均数的求法求解.(2)结合题意完成列联表,并求出
,然后再根据频率分布直方图中平均数的求法求解.(2)结合题意完成列联表,并求出![]() ,与临界值表对照后可得结论.(3)根据题意得不经常参加社会实践活动的有
,与临界值表对照后可得结论.(3)根据题意得不经常参加社会实践活动的有![]() 人,其中成绩优秀的有1人,然后根据古典概型概率的求法求解.
人,其中成绩优秀的有1人,然后根据古典概型概率的求法求解.
详解:(1)由题意得活动时间在![]() 的频率为
的频率为![]() ,
,
又参加社会实践活动的时间在![]() 内的有
内的有![]() 人,
人,
所以样本容量![]() .
.
根据频率分布直方图,该校学生每周参加社会实践活动时间的平均值为:
![]()
![]() (小时).
(小时).
(2)由题意得“不经常参加社会实践”的学生有![]() 人,
人,
所以列联表如下:
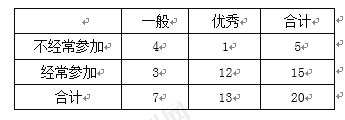
由表中数据可得![]() .
.
所以在犯错误的概率不超过![]() 的前提下可以认为“青少年科技创新大赛成绩优秀与经常参加社会实践活动有关系”.
的前提下可以认为“青少年科技创新大赛成绩优秀与经常参加社会实践活动有关系”.
(3)由(2)知不经常参加社会实践活动的有![]() 人,其中成绩优秀的有1人.
人,其中成绩优秀的有1人.
设成绩优秀的编号为![]() ;成绩一般的学生有
;成绩一般的学生有![]() 人,编号依次为
人,编号依次为![]() .
.
所有参加培训的情况有:![]()
![]() ,共10种.
,共10种.
恰好一人成绩优秀的情况有![]() ,共4种.
,共4种.
所以由古典概型计算公式得所求概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() 为常数,且
为常数,且![]() ).
).
(1)若当![]() 时,函数
时,函数![]() 与
与![]() 的图象有且只要一个交点,试确定自然数
的图象有且只要一个交点,试确定自然数![]() 的值,使得
的值,使得![]() (参考数值
(参考数值![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)当![]() 时,证明:
时,证明:![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地拟规划种植一批芍药,为了美观,将种植区域(区域I)设计成半径为1km的扇形![]() ,中心角
,中心角![]() (
(![]() ).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形
).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形![]() ,其中点
,其中点![]() ,
,![]() 分别在边
分别在边![]() 和
和![]() 上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
(1)要使观赏区的年收入不低于5万元,求![]() 的最大值;
的最大值;
(2)试问:当![]() 为多少时,年总收入最大?
为多少时,年总收入最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 且
且![]() .
.
(1)若函数![]() 在
在![]() 上恒有意义,求
上恒有意义,求![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 上为增函数,且最大值为
上为增函数,且最大值为![]() ?若存在求出
?若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,有下列结论:
,有下列结论:
①![]() 的定义域为(-1, 1); ②
的定义域为(-1, 1); ②![]() 的值域为(
的值域为(![]() ,
, ![]() );
);
③![]() 的图象关于原点成中心对称; ④
的图象关于原点成中心对称; ④![]() 在其定义域上是减函数;
在其定义域上是减函数;
⑤对![]() 的定义城中任意
的定义城中任意![]() 都有
都有![]() .
.
其中正确的结论序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公园有三条观光大道![]() 围成直角三角形,其中直角边
围成直角三角形,其中直角边![]() ,斜边
,斜边![]() .现有甲、乙、丙三位小朋友分别在
.现有甲、乙、丙三位小朋友分别在![]() 大道上嬉戏,所在位置分别记为点
大道上嬉戏,所在位置分别记为点![]() .
.
(1)若甲乙都以每分钟![]() 的速度从点
的速度从点![]() 出发在各自的大道上奔走,到大道的另一端
出发在各自的大道上奔走,到大道的另一端
时即停,乙比甲迟2分钟出发,当乙出发1分钟后,求此时甲乙两人之间的距离;
(2)设![]() ,乙丙之间的距离是甲乙之间距离的2倍,且
,乙丙之间的距离是甲乙之间距离的2倍,且![]() ,请将甲
,请将甲
乙之间的距离![]() 表示为θ的函数,并求甲乙之间的最小距离.
表示为θ的函数,并求甲乙之间的最小距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,在极坐标系(与平面直角坐标系
,在极坐标系(与平面直角坐标系![]() 取相同的长度,以原点
取相同的长度,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴)中,曲线
轴的非负半轴为极轴)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程与曲线
的参数方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com