
【题目】三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,点F为棱
,点F为棱![]() 的中点,点E为线段
的中点,点E为线段![]() 上的动点.
上的动点.
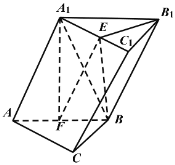
(1)求证:![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)首先根据题意得到![]() ,利用平面
,利用平面![]() 平面
平面![]() 的性质得到
的性质得到![]() 平面
平面![]() ,从而得到
,从而得到![]() ,根据勾股定理得到
,根据勾股定理得到![]() ,从而得到
,从而得到![]() ,利用线面垂直的判定得到
,利用线面垂直的判定得到![]() 平面
平面![]() ,从而证明
,从而证明![]() .
.
(2)以点![]() 为原点,以
为原点,以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,利用向量法求解二面角
轴,建立空间直角坐标系,利用向量法求解二面角![]() 的余弦值即可.
的余弦值即可.
(1)因为![]() ,
,![]() 为
为![]() 中点,所以
中点,所以![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,故
,故![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
又因为在三棱柱![]() 中,
中,![]() ,
,
所以![]() ,
,![]() ,
,
又![]() ,故
,故![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)以点![]() 为原点,以
为原点,以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴,
轴,
建立如图所示的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
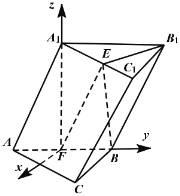
设![]() ,由
,由![]() 得:
得:![]() ,
,
又![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
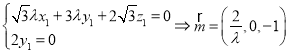 ,
,
因为![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则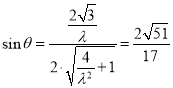 ,
,
解得:![]() .
.
又平面![]() 的一个法向量
的一个法向量![]() ,
,
又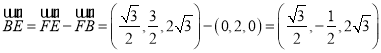 ,
,
![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则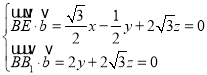 ,
,
则平面![]() 的一个法向量为
的一个法向量为![]()
设二面角![]() 的平面角为
的平面角为![]() ,
,
则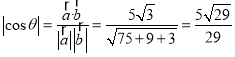 ,
,
又因为二面角![]() 的平面角为锐角,
的平面角为锐角,
则二面角![]() 的余弦值为
的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】第23届冬季奥运会于2018年2月9日至2月25日在韩国平昌举行,期间正值我市学校放寒假,寒假结束后,某校工会对全校教职工在冬季奥运会期间每天收看比赛转播的时间作了一次调查,得到如下频数分布表:
收看时间(单位:小时) |
|
|
|
|
|
|
收看人数 | 14 | 30 | 16 | 28 | 20 | 12 |
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“体育达人”,否则定义为“非体育达人”,请根据频数分布表补全![]() 列联表:
列联表:
| 男 | 女 | 合计 |
体育达人 | 40 | ||
非体育达人 | 30 | ||
合计 |
并判断能否有![]() 的把握认为该校教职工是否为“体育达人”与“性别”有关;
的把握认为该校教职工是否为“体育达人”与“性别”有关;
(2)在全校“体育达人”中按性别分层抽样抽取6名,再从这6名“体育达人”中选取2名作冬奥会知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“克拉茨猜想”又称“![]() 猜想”,是德国数学家洛萨克拉茨在
猜想”,是德国数学家洛萨克拉茨在![]() 年世界数学家大会上公布的一个猜想:任给一个正整数
年世界数学家大会上公布的一个猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半;如果
是偶数,就将它减半;如果![]() 为奇数就将它乘
为奇数就将它乘![]() 加
加![]() ,不断重复这样的运算,经过有限步后,最终都能够得到
,不断重复这样的运算,经过有限步后,最终都能够得到![]() ,得到
,得到![]() 即终止运算,己知正整数
即终止运算,己知正整数![]() 经过
经过![]() 次运算后得到
次运算后得到![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() D.
D.![]() 或
或![]() 或
或![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》是中国最古老的天文学和数学著作,书中提到:从冬至之日起,小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气的日影子长依次成等差数列,若冬至、立春、春分的日影子长的和是37.5尺,芒种的日影子长为4.5尺,则立夏的日影子长为:( )
A.15.5尺B.12.5尺C.9.5尺D.6.5尺
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com