
分析 (1)先根据题意先表示出点P受光源A的照度和受光源B的照度再根据光源A与光源B在点P产生相等的照度建立方程,即可求点P的“总照度”I(x)的函数表达式;
(2)利用导数先研究函数的极值,然后根据函数的单调性求出函数的最小值即可.
解答 解:(1)由题意知,若a=8,b=1,d=3,则点P受光源A的照度为k•$\frac{8}{{x}^{2}}$,
受光源B的照度为k•$\frac{1}{(3-x)^{2}}$;
点P的“总照度”I(x)=k•$\frac{8}{{x}^{2}}$+k•$\frac{1}{(3-x)^{2}}$,(0<x<3);
(2)I′(x)=k•[-$\frac{16}{{x}^{3}}$+$\frac{2}{(3-x)^{3}}$]=k•$\frac{18(x-2)({x}^{2}-6x+12)}{{x}^{3}(3-x)^{3}}$,
令I′(x)=0,解得:x=2,
列表:
| x | (0,2) | 2 | (2,3) |
| I′(x) | - | 0 | + |
| I(x) | 减 | 极小值 | 增 |
点评 本题主要考查了函数模型的选择与应用,同时考查了函数的最值的求解,导数法求函数最值是常用的方法,属于中档题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{3}$,π) | B. | ($\frac{π}{3}$,π] | C. | [$\frac{π}{3}$,π] | D. | (0,$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
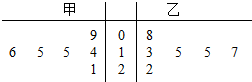
| A. | ${\overline{x}}_{1}$>${\overline{x}}_{2}$,s${\;}_{1}^{2}$<${s}_{2}^{2}$ | B. | ${\overline{x}}_{1}$=${\overline{x}}_{2}$,s${\;}_{1}^{2}$>${s}_{2}^{2}$ | ||
| C. | ${\overline{x}}_{1}$=${\overline{x}}_{2}$,s${\;}_{1}^{2}$=${s}_{2}^{2}$ | D. | ${\overline{x}}_{1}$=${\overline{x}}_{2}$,s${\;}_{1}^{2}$<${s}_{2}^{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com