
 ,函数
,函数
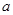 =4,求函数
=4,求函数 的反函数
的反函数 ;
;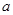 的不同取值,讨论函数
的不同取值,讨论函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.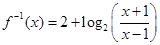 ,
,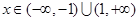 ;(2)
;(2)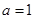 时
时 为奇函数,当
为奇函数,当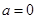 时
时 为偶函数,当
为偶函数,当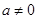 且
且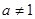 时
时 为非奇非偶函数.
为非奇非偶函数.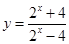 作为关于
作为关于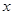 的方程,解出
的方程,解出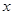 ,得
,得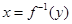 ,再把此式中的
,再把此式中的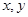 互换,即得反函数的解析式,还要注意的是一般要求出原函数的值域,即为反函数的定义域;(2)讨论函数的奇偶性,我们可以根据奇偶性的定义求解,在
互换,即得反函数的解析式,还要注意的是一般要求出原函数的值域,即为反函数的定义域;(2)讨论函数的奇偶性,我们可以根据奇偶性的定义求解,在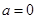 ,
,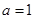 这两种情况下,由奇偶性的定义可知函数
这两种情况下,由奇偶性的定义可知函数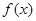 具有奇偶性,在
具有奇偶性,在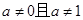 时,函数的定义域是
时,函数的定义域是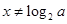 ,不关于原点对称,因此函数既不是奇函数也不是偶函数.
,不关于原点对称,因此函数既不是奇函数也不是偶函数.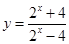 ,解得
,解得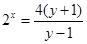 ,从而
,从而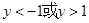 ,
,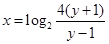
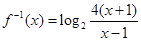 ,
,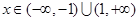
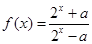 且
且
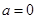 时,
时,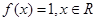 ,
,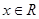 都有
都有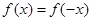 ,∴
,∴ 为偶函数
为偶函数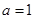 时,
时,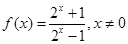 ,
,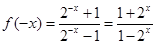 ,
,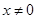 且
且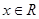 都有
都有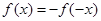 ,∴
,∴ 为奇函数
为奇函数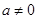 且
且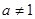 时,定义域为
时,定义域为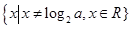 ,
, 为非奇非偶函数
为非奇非偶函数

科目:高中数学 来源:不详 题型:单选题
|
| f(x1)-f(x2) |
| x1-x2 |
A.(0,
| B.(0,1) | C.[
| D.(0,3) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,则f(log220)的值为( )
,则f(log220)的值为( )| A.1 | B.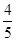 | C.-1 | D.-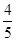 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.①② | B.②④ | C.①②③ | D.①②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com