
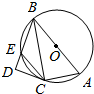
 如图,在△ABC中,∠ACB=90°,AB=2AC=8,作△ABC外接圆O的切线CD,作BD⊥CD于D,交圆O于点E,给出下列四个结论:①∠BCD=60°;②DE=2;③BC2=BD•BA;④CE∥AB;则其中正确的序号是①②③④.
如图,在△ABC中,∠ACB=90°,AB=2AC=8,作△ABC外接圆O的切线CD,作BD⊥CD于D,交圆O于点E,给出下列四个结论:①∠BCD=60°;②DE=2;③BC2=BD•BA;④CE∥AB;则其中正确的序号是①②③④. 分析 利用直角△ABC的边角关系即可得出BC,利用弦切角定理可得∠BCD=∠A=60°.利用直角△BCD的边角关系即可得出CD,BD.再利用切割线定理可得CD2=DE•DB,即可得出DE.利用△ACB∽△CDB,可得BC2=BD•BA;证明∠BCE=∠ABC,可得CE∥AB
解答 解:在△ABC中,∠C=90°,∠A=60°,AB=8,∴BC=AB•sin60°=4$\sqrt{3}$.
∵CD是此圆的切线,∴∠BCD=∠A=60°,即①正确.
在Rt△BCD中,CD=BC•cos60°=2$\sqrt{3}$,BD=BC•sin60°=6.
由切割线定理可得CD2=DE•DB,∴12=6DE,解得DE=2,即②正确.
∵∠BCD=∠A,∠D=∠ACB,∴△ACB∽△CDB,∴CB:DB=AB:CB,∴BC2=BD•BA,即③正确;
④∵∠ECD=∠ABC=30°,∠BCD=60°,∴∠BCE=30°=∠ABC,∴CE∥AB,即④正确;
故答案为:①②③④.
点评 熟练掌握直角三角形的边角关系、弦切角定理、切割线定理是解题的关键.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:选择题
| A. | (5,10) | B. | (5,+∞) | C. | (-∞,5) | D. | (10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log2(x+1) | B. | y=log2(x-1) | C. | y=log2x+1 | D. | y=log2x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=${3^{\frac{1}{x+1}}}$ | B. | y=${2^{-\frac{x}{2}}}$ | C. | y=x2+x+1 | D. | y=$\sqrt{1-{2}^{x}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com