
| A. | an=2n-2 | B. | an=n2+n-2 | ||
| C. | an=$\left\{\begin{array}{l}{0,}&{n=1}\\{2n-1,}&{n≥2}\end{array}\right.$ | D. | an=$\left\{\begin{array}{l}{0,}&{n=1}\\{2n,}&{n≥2}\end{array}\right.$ |
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
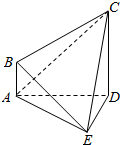 如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=3AB.
如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=3AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
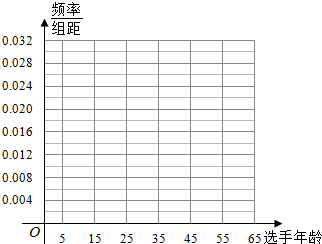 《中国梦想秀》是浙江卫士推出的一档“真人秀”综艺节目,节目开播至今,有上百组的追梦人在这个舞台上实现了自己的梦想,某机构随机抽取100名参与节目的选手,以他们的年龄作为样本进行分析研究,并根据所得数据作出如下频数分布表:
《中国梦想秀》是浙江卫士推出的一档“真人秀”综艺节目,节目开播至今,有上百组的追梦人在这个舞台上实现了自己的梦想,某机构随机抽取100名参与节目的选手,以他们的年龄作为样本进行分析研究,并根据所得数据作出如下频数分布表:| 选手年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 频数 | 6 | 22 | 32 | 24 | 10 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com