解:(I)对函数求导数,得f'(x)=1-
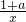
∵在x=1时,函数存在极值.
∴f'(1)=1-
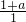
=-a=0,可得a=0;
(II)当x>1时,,
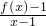
<

lnx等价于(x+1)lnx-2x+2>0…(*)
设F(x)=(x+1)lnx-2x+2,得F'(x)=

+lnx-1
再设G(x)=

+lnx-1,得G'(x)=-

+

=

∵x>1,∴G'(x)=

>0,得G(x)是(1,+∞)上的增函数
因此G(x)>G(1)=0,即F'(x)>0区间(1,+∞)上恒成立
∴F(x)=(x+1)lnx-2x+2是(1,+∞)上的增函数,得F(x)>F(1)=0
因此,不等式(*)在区间(1,+∞)上恒成立,即当x>1时,
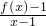
<

lnx恒成立.
分析:(I)对函数求导数,得f'(x)=1-
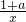
,根据函数在极值点处导数值为零列式,解之得a=0;
(II)原不等式等价于(x+1)lnx-2x+2>0.因此构造函数F(x)=(x+1)lnx-2x+2,通过研究F'(x)的单调性,得到F'(x)是(1,+∞)上的增函数,从而得到F'(x)>F'(1)=0在区间(1,+∞)上恒成立,得F(x)是(1,+∞)上的增函数,得F(x)>F(1)=0,从而证出原不等式成立.
点评:本题给出含有对数的函数,在已知极值的情况下求参数a的值,并证明一个恒成立的不等式,着重考查了利用导数研究函数的单调性和不等式恒成立的证明等知识,属于中档题.

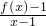 <
< lnx.
lnx.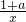
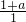 =-a=0,可得a=0;
=-a=0,可得a=0;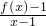 <
< lnx等价于(x+1)lnx-2x+2>0…(*)
lnx等价于(x+1)lnx-2x+2>0…(*) +lnx-1
+lnx-1 +lnx-1,得G'(x)=-
+lnx-1,得G'(x)=- +
+ =
=
 >0,得G(x)是(1,+∞)上的增函数
>0,得G(x)是(1,+∞)上的增函数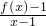 <
< lnx恒成立.
lnx恒成立.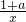 ,根据函数在极值点处导数值为零列式,解之得a=0;
,根据函数在极值点处导数值为零列式,解之得a=0;

 阶梯计算系列答案
阶梯计算系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<