练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在平面上，我们如果用一条直线去截正方形的一个角，那么截下的一个直角三角形，按图所标边长，由勾股定理有：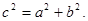

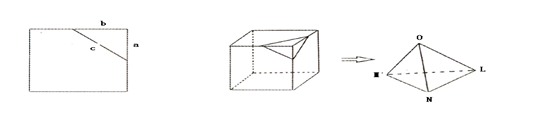
    设想正方形换成正方体，把截线换成如图的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥O—LMN，如果用表示三个侧面面积，表示截面面积，那么你类比得到的结论是                    .

     

    解析试题分析：解建立从平面图形到空间图形的类比，于是作出猜想：S42=S12+S22+S32，故填
    考点：本题考查了类比推理的运用
    点评：此类问题主要考查学生的知识量和知识迁移、类比的基本能力，属基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    已知整数对的序列如下：（1，1），（1，2），（2，1），（1，3），（2，2），（3，1）（1，4），（2，3），（3，2），（4，1）……则第2011个数对是          

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知命题“设是正实数，如果，则有”，用类比思想推广“设是正数，如果则有 __________

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知“凡是9的倍数的自然数都是3的倍数”和“自然数是9的倍数”，根据三段论推理规则，我们可以得到的结论是　　 　　．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    （文科） 给出下列等式： ， ，  ， ……
    请从中归纳出第个等式：   ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    用反证法证明命题“a，b∈N，ab可被5整除，那么a，b中至少有一个能被5整除”，那么反设的内容是________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

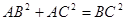    在平面几何里，有勾股定理：“设的两边AB、AC互相垂直，则。”拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面积与底面积间的关系，可以得到的正确结论是：“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直，则                            ”。

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

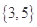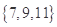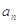    有一个奇数列1, 3, 5, 7, 9，…，现在进行如下分组：第一组含一个数，第二组含两个数，第三组含三个数，第四组含四个数，…，现观察猜想每组内各数之和为与其组的编号数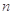的关系为          .

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    从1=1，1-4=-(1+2),1-4+9=1+2+3,1-4+9-16=-(1+2+3+4),…,推广到第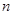个等式为
    ___________________       

    查看答案和解析>>

    同步练习册答案