
已知函数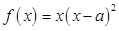 ,
,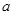 是大于零的常数.
是大于零的常数.
(Ⅰ)当 时,求
时,求 的极值;
的极值;
(Ⅱ)若函数 在区间
在区间 上为单调递增,求实数
上为单调递增,求实数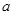 的取值范围;
的取值范围;
(Ⅲ)证明:曲线 上存在一点
上存在一点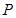 ,使得曲线
,使得曲线 上总有两点
上总有两点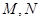 ,且
,且 成立.
成立.
(I)极大值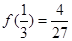 ,极小值
,极小值 .
.
(Ⅱ)当函数 在区间
在区间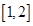 上为单调递增时,
上为单调递增时, 或
或 .
.
(Ⅲ)曲线 上存在一点
上存在一点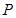
 ,使得曲线
,使得曲线 上总有两点
上总有两点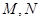 ,且
,且 成立 .
成立 .
解析试题分析:(I)求极值一般遵循“求导数、求驻点、讨论区间的导数值正负、计算极值”.
(Ⅱ)函数 在区间
在区间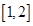 上为单调递增,因此,其导函数为正数恒成立,据此建立
上为单调递增,因此,其导函数为正数恒成立,据此建立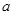 的不等式求解.
的不等式求解.
应注意结合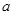 的不同取值情况加以讨论.
的不同取值情况加以讨论.
(Ⅲ)通过确定函数的极大值、极小值点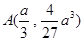 ,
, , 并确定
, 并确定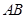 的中点
的中点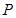
 .
.
设 是图象任意一点,由
是图象任意一点,由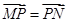 ,可得
,可得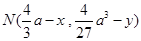 ,
,
根据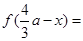
 ,可知点
,可知点 在曲线
在曲线 上,作出结论.
上,作出结论.
本题难度较大,关键是能否认识到极大值、极小值点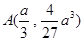 ,
, 的中点即为所求.
的中点即为所求.
试题解析:(I)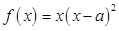 ,
, ,
,
当 时,
时, ,
,
令 得
得 .
. 在
在 分别单调递增、单调递减、单调递增,
分别单调递增、单调递减、单调递增,
于是,当 时,函数有极大值
时,函数有极大值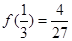 ,
, 时,有极小值
时,有极小值 .
.
------4分
(Ⅱ)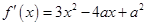 ,若函数
,若函数 在区间
在区间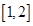 上为单调递增,
上为单调递增,
则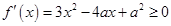 在
在 上恒成立,
上恒成立,
当 ,即
,即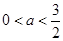 时,由
时,由 得
得 ;
;
当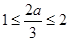 ,即
,即 时,
时, ,无解;
,无解;
当 ,即
,即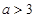 时,由
时,由 得
得 .
.
综上,当函数 在区间
在区间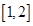 上为单调递增时,
上为单调递增时, 或
或 . 10分
. 10分
(Ⅲ)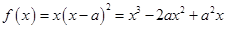 ,
,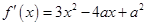 ,
,
令 ,得
,得 ,
,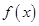 在区间
在区间 ,
, ,
, 上分别单调递增,单调递减,单调递增,
上分别单调递增,单调递减,单调递增,
于是当 时,有极大值
时,有极大值 ;
;
当 时,有极小值
时,有极小值 .
.
记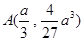 ,
, ,
, 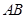 的中点
的中点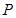
 ,
,
设 是图象任意一点,由
是图象任意一点,由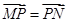 ,得
,得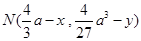 ,
,
因为
 ,
,
由此可知点


科目:高中数学 来源: 题型:解答题
已知函数
(I)当a=1时,求函数f(x)的最小值;
(II)当a≤0时,讨论函数f(x)的单调性;
(III)是否存在实数a,对任意的x1,x2 (0,+∞),且x1≠x2,都有
(0,+∞),且x1≠x2,都有 恒成立.若存在,求出a的取值范围;若不存在,说明理由.
恒成立.若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知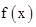 是二次函数,不等式
是二次函数,不等式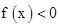 的解集是(0,5),且f(x)在区间[-1,4]上的最大值是12.
的解集是(0,5),且f(x)在区间[-1,4]上的最大值是12.
(1)求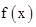 的解析式;
的解析式;
(2)是否存在自然数m,使得方程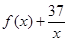 =0在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
=0在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数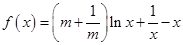 ,(其中常数
,(其中常数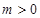 ).
).
(1)当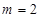 时,求
时,求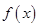 的极大值;
的极大值;
(2)试讨论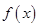 在区间
在区间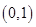 上的单调性;
上的单调性;
(3)当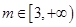 时,曲线
时,曲线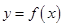 上总存在相异两点
上总存在相异两点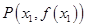 、
、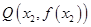 ,使得曲线
,使得曲线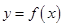 在点
在点 、
、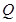 处的切线互相平行,求
处的切线互相平行,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数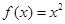 ,
,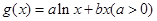 .
.
(Ⅰ)若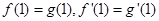 ,求
,求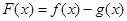 的极小值;
的极小值;
(Ⅱ)在(Ⅰ)的结论下,是否存在实常数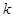 和
和 ,使得
,使得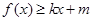 和
和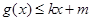 ?若存在,求出
?若存在,求出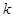 和
和 的值.若不存在,说明理由.
的值.若不存在,说明理由.
(Ⅲ)设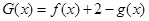 有两个零点
有两个零点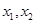 ,且
,且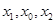 成等差数列,试探究
成等差数列,试探究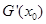 值的符号.
值的符号.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某出版社新出版一本高考复习用书,该书的成本为5元/本,经销过程中每本书需付给代理商m元(1≤m≤3)的劳务费,经出版社研究决定,新书投放市场后定价为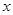 元/本(9≤
元/本(9≤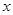 ≤11),预计一年的销售量为
≤11),预计一年的销售量为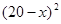 万本.
万本.
(1)求该出版社一年的利润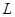 (万元)与每本书的定价
(万元)与每本书的定价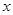 的函数关系式;
的函数关系式;
(2)当每本书的定价为多少元时,该出版社一年的利润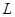 最大,并求出
最大,并求出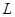 的最大值
的最大值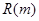 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com