
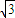 <l<2
<l<2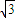 .
.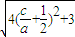 ,由次形式推断出线段长度范围的关键是确定
,由次形式推断出线段长度范围的关键是确定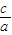 的范围,由此问题研究的方向找到,以下依据a>b>c且a+b+c=0恒等变形求
的范围,由此问题研究的方向找到,以下依据a>b>c且a+b+c=0恒等变形求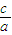 的范围即可.
的范围即可.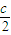 )2+
)2+ c2]>0.
c2]>0.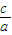 >-2.
>-2.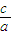 <-
<- .
.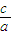 <-
<- .
.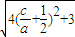 .
.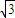 ,2
,2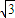 ).
).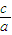 的范围,此类技巧的运用需要平时经验的积累,以及数学素养的提高,题后应对这些变形的技巧的变形过程及变形后达到目标进行细致的分析,力争能把握此类技巧的使用.
的范围,此类技巧的运用需要平时经验的积累,以及数学素养的提高,题后应对这些变形的技巧的变形过程及变形后达到目标进行细致的分析,力争能把握此类技巧的使用. 

科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com