
【题目】
如图所示,正方形![]() 与矩形
与矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() .
.
(1)若点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
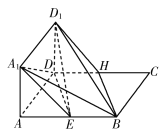
【答案】见解析
【解析】
(1)四边形ADD1A1为正方形,连接AD1,设A1D∩AD1=F,则F是AD1的中点,
又点E为AB的中点,连接EF,则EF为△ABD1的中位线,所以EF∥BD1.
又BD1![]() 平面A1DE,EF平面A1DE,所以BD1∥平面A1DE.(3分)
平面A1DE,EF平面A1DE,所以BD1∥平面A1DE.(3分)
因为BH//DE,且DE平面A1DE,BH![]() 平面A1DE,所以BH∥平面A1DE,
平面A1DE,所以BH∥平面A1DE,
又BD1![]() BH=B,所以平面
BH=B,所以平面![]() 平面
平面![]() .(5分)
.(5分)
(2)根据题意,得DD1⊥DA,D1D⊥DC,AD⊥DC,则以D为坐标原点,DA,DC,DD1所在直线分别为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,如图所示,
,如图所示,
则D(0,0,0),D1(0,0,1),C(0,2,0).(7分)
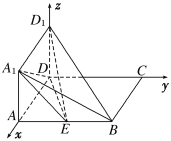
假设满足条件的点E存在,且点E的纵坐标为![]() ,则E(1,
,则E(1,![]() ,0)(0≤
,0)(0≤![]() ≤2),
≤2),
![]() =(-1,2-
=(-1,2-![]() ,0),
,0),![]() =(0,2,-1),
=(0,2,-1),
设![]() =(x1,y1,z1)是平面D1EC的法向量,则
=(x1,y1,z1)是平面D1EC的法向量,则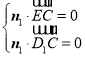 ,即
,即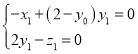 ,
,
令![]() =1,则平面D1EC的一个法向量为
=1,则平面D1EC的一个法向量为![]() =(2-
=(2-![]() ,1,2).(9分)
,1,2).(9分)
由题意,知平面DEC的一个法向量为![]() =(0,0,1).(10分)
=(0,0,1).(10分)
由二面角![]() 的大小为
的大小为![]() ,得
,得![]() =
=![]() =
=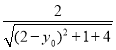 =
=![]() ,
,
解得![]() =
=![]()
![]() [0,2].
[0,2].
所以在线段![]() 上不存在一点
上不存在一点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() .(12分)
.(12分)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列几个命题:
①函数y= ![]() +
+ ![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
②方程x2+(a﹣3)x+a=0的有一个正实根,一个负实根,则a<0;
③f(x)是定义在R上的奇函数,当x<0时,f(x)=2x2+x﹣1,则x≥0时,f(x)=﹣2x2+x+1
④函数y= ![]() 的值域是(﹣1,
的值域是(﹣1, ![]() ).
).
其中正确命题的序号有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1: 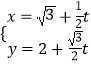 (t为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4.
(t为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4.
(1)求出曲线C2的直角坐标方程;
(2)若C1与C2相交于A,B两点,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知椭圆![]() 的右焦点为
的右焦点为![]() ,以椭圆
,以椭圆![]() 与双曲线
与双曲线![]() 两条渐近线的四个交点为顶点的四边形的面积为
两条渐近线的四个交点为顶点的四边形的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 为椭圆
为椭圆![]() 上的两点(
上的两点(![]() 不同时在
不同时在![]() 轴上),点
轴上),点![]() ,证明:存在实数
,证明:存在实数![]() ,当
,当![]() 三点共线时,
三点共线时,![]() 为常数.
为常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在[﹣1,1]的函数满足f(﹣x)=﹣f(x),当a,b∈[﹣1,0)时,总有 ![]() >0(a≠b),若f(m+1)>f(2m),则实数m的取值范围是 .
>0(a≠b),若f(m+1)>f(2m),则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
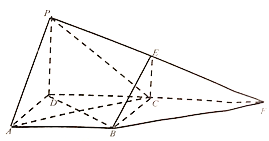
【题目】如图, ![]() 为正方形,
为正方形, ![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() .
.
(1)若![]() 和
和![]() 延长交于点
延长交于点![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 边上的动点,求直线
边上的动点,求直线![]() 与平面
与平面![]() 所成角正弦值的最小值.
所成角正弦值的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z1= ![]() +(a2﹣3)i,z2=2+(3a+1)i(a∈R,i是虚数单位).
+(a2﹣3)i,z2=2+(3a+1)i(a∈R,i是虚数单位).
(1)若复数z1﹣z2在复平面上对应点落在第一象限,求实数a的取值范围;
(2)若虚数z1是实系数一元二次方程x2﹣6x+m=0的根,求实数m值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com