Question

已知半径为1的定圆⊙P的圆心P到定直线的距离为2，Q是上一动点，⊙Q与⊙P相外切，⊙Q交于M、N两点，对于任意直径MN，平面上恒有一定点A，使得∠MAN为定值。求∠MAN的度数。

Answer 1

60°

解析:

以为x轴，点P到的垂线为y轴建立如图所示的直角坐标系，设Q的坐标为(x, 0)，点A(k, λ)，⊙Q的半径为r，则：M(x-r, 0), N(x+r, 0), P(2, 0), PQ==1+r。所以x=±, ∴tan∠MAN=

，令2m=h²+k²-3，tan∠MAN=，所以m+rk=nhr，∴m+(1-nh)r=，两边平方，得：m²+2m(1-nh)r-(1-nh)²r²=k²r²+2k²r-3k²，因为对于任意实数r≥1，上式恒成立，所以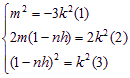，由（1）（2）式，得m=0, k=0，由（3）式，得n=。由2m=h²+k²-3得h=±，所以tan∠MAN==h=±。所以∠MAN=60°或120°（舍）（当Q(0, 0), r=1时∠MAN=60°），故∠MAN=60°。