【题目】如图，在棱长为1的正方体
中，点P在线段
上运动，给出以下四个命题：
①异面直线
与
所成的角为定值；
②二面角
的大小为定值；
③三棱锥
的体积为定值；
其中真命题的个数为（ ）
A.0B.1C.2D.3
【答案】D
【解析】
对于①由题意及图形利用异面直线所成角的概念及求异面直线间的方法及可求解；对于②由题意及平面具有延展性可知实质为平面
与平面
所成的二面角；对于③由题意及三棱锥的体积的算法中可以进行顶点可以轮换求解体积，和点P的位置及直线
与平面的位置即可判断正误．
解：对于①因为在棱长为1的正方体
中，
点P在线段上运动，有正方体的及题意易有
平面，
而
平面，所以
，
故这两个异面直线所成的角为定值
，所以①正确；
对于②因为二面角
的大小，
实质为平面与平面所成的二面角而这两的平面为固定的不变的平面所以夹角也为定值，故②正确；
对于③三棱锥
的体积还等于三棱锥的体积
的体积，
而平面
为固定平面且大小一定，又因为
，而
平面，
所以点A到平面DBC1的距离即为点P到该平面的距离，
所以三棱锥的体积为定值，故③正确．
故选：D．
科目：高中数学 来源： 题型：
【题目】
如图，在三棱锥P—ABC中，PC⊥底面ABC，AB⊥BC，D，E分别是AB，PB的中点．
（Ⅰ）求证：DE∥平面PAC．
（Ⅱ）求证：AB⊥PB；
（Ⅲ）若PC＝BC，求二面角P—AB—C的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，曲线
的参数方程为
（
为参数），直线
的参数方程为
（
为参数）.
（Ⅰ）若
，求直线被曲线截得的线段的长度；
（Ⅱ）若
，在曲线上求一点
，使得点到直线的距离最小，并求出最小距离.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（Ⅰ）求过点A（2，6）且在两坐标轴上的截距相等的直线m的方程；
（Ⅱ）求过点A（2，6）且被圆C：（x﹣3）2+（y﹣4）2＝4截得的弦长为
的直线l的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地区某农产品近几年的产量统计如表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
（Ⅰ）根据表中数据，建立
关于的线性回归方程
；
（Ⅱ）根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据
，其回归直线的斜率和截距的最小二乘估计分别为：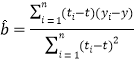
，
.(参考数据:
，计算结果保留小数点后两位）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从某居民区随机抽取10个家庭，获得第
个家庭的月收入
（单位：千元）与月储蓄
（单位：千元）的数据资料，算得
， 
，
， 
(1).求家庭的月储蓄
对月收入
的线性回归方程
；
(2).判断变量
与
之间的正相关还是负相关；
(3).若该居民区某家庭月收入为7千元，预测该家庭的月储蓄.
附：回归直线的斜率和截距的最小二乘估计公式分别为
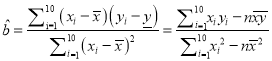
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出以下四个说法：
①残差点分布的带状区域的宽度越窄相关指数越小
②在刻画回归模型的拟合效果时，相关指数
的值越大，说明拟合的效果越好；
③在回归直线方程
中，当解释变量
每增加一个单位时，预报变量
平均增加
个单位；
④对分类变量
与
，若它们的随机变量
的观测值
越小，则判断“与有关系”的把握程度越大．
其中正确的说法是
A. ①④B. ②④C. ①③D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
