
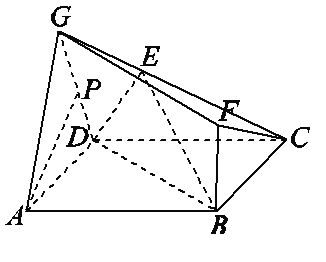
【题目】如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,BF⊥平面ABCD,∠GDC=90°,点E是线段GC上除两端点外的一点,若点P为线段GD的中点.
(Ⅰ)求证:AP⊥平面GCD;
(Ⅱ)求证:平面ADG∥平面FBC;
(Ⅲ)若AP∥平面BDE,求![]() 的值.
的值.
【答案】(1)见解析(2)见解析(3)2
【解析】试题分析:(1) 因为△GAD是等边三角形,点P为线段GD的中点,故AP⊥GD,又CD⊥平面GAD,所以CD⊥AP,从而AP⊥平面GCD.;(2) ∵BF⊥平面ABCD,∴BF⊥CD,又CD∩GD=D, ∴CD⊥平面FBC,结合(1)可证明结果;(3) 连接PC交DE于点M,连接AC交BD于点O,连接OM,∵AP∥平面BDE,AP∥OM,从而M是PC中点,过P作PN∥DE,交CG于点N,
则N是GE中点,E是CN中点.
试题解析:
(Ⅰ)证明:因为△GAD是等边三角形,点P为线段GD的中点,故AP⊥GD,
因为AD⊥CD,GD⊥CD,且AD∩GD=D,AD,GD平面GAD,故CD⊥平面GAD,
又AP平面GAD,故CD⊥AP,
又CD∩GD=D,CD,GD平面GCD,故AP⊥平面GCD.
(Ⅱ)证明:∵BF⊥平面ABCD,∴BF⊥CD,
∵BC⊥CD,BF∩BC=B,BF,BC平面FBC,∴CD⊥平面FBC,
由(Ⅰ)知CD⊥平面GAD,∴平面ADG∥平面FBC.
(Ⅲ)解:连接PC交DE于点M,连接AC交BD于点O,连接OM,
∵AP∥平面BDE,AP∥OM,
∵O是AC中点,∴M是PC中点
过P作PN∥DE,交CG于点N,
则N是GE中点,E是CN中点,∴![]() =2.
=2.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】已知一个动圆与两个定圆![]() 和
和![]() 均相切,其圆心的轨迹为曲线C.
均相切,其圆心的轨迹为曲线C.
(1) 求曲线C的方程;
(2) 过点F(![]() )做两条可相垂直的直线
)做两条可相垂直的直线![]() ,设
,设![]() 与曲线C交于A,B两点,
与曲线C交于A,B两点, ![]() 与曲线 C交于C,D两点,线段AC,BD分别与直线
与曲线 C交于C,D两点,线段AC,BD分别与直线![]() 交于M,M,N两点。求证|MF|:|NF|为定值.
交于M,M,N两点。求证|MF|:|NF|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线T的焦点为F,准线为l,过F的直线m与T交于A,B两点,C,D分别为A,B在l上的射影,M为AB的中点,若m与l不平行,则△CMD是( )
A. 等腰三角形且为锐角三角形
B. 等腰三角形且为钝角三角形
C. 等腰直角三角形
D. 非等腰的直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b分别是△ABC内角A,B的对边,且bsin2A=![]() acos Asin B,函数f(x)=sin Acos2x-sin2
acos Asin B,函数f(x)=sin Acos2x-sin2![]() sin 2x,x∈
sin 2x,x∈![]() .
.
(1)求A;
(2)求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x+3|-|2x-a|,a∈R.
(1)若不等式f(x)≤-5的解集非空,求实数a的取值范围;
(2)若函数y=f(x)的图象关于点![]() 对称,求实数a的值.
对称,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲](10分)
已知函数f(x)=2|x-2|+3|x+3|.
(Ⅰ)解不等式:f(x)>15;
(Ⅱ)若函数f(x)的最小值为m,正实数a,b满足4a+25b=m,求![]() +
+![]() 的最小值,并求出此时a,b的大小.
的最小值,并求出此时a,b的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x+1|+|x+1|.
(Ⅰ)求不等式f(x)≤8的解集;
(Ⅱ)若不等式f(x)>|a-2|对任意x∈R恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三文科班学生参加了数学与地理水平测试,学校从测试合格的学生中随机抽取100人的成绩进行统计分析.抽取的100人的数学与地理的水平测试成绩如下表:

成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人.
(1)若在该样本中,数学成绩优秀率为30%,求a,b的值;
(2)若样本中![]() ,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com