在递减等比数列{an}中,a1+a4=9,a2a3=8,则S6=________.
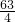
分析:根据等比数列的性质,得到a
2a
3=a
1a
4=8,又a
1+a
4=9,两者联立可求出a
1和a
4的值,进而求出公比q的值,利用等比数列的求和公式表示出S
6,把a
1及q的值代入即可求出值.
解答:∵a
2a
3=a
1a
4=8,a
1+a
4=9,且数列{a
n}为递减数列,
∴a
1=8,a
4=1,
又a
4=a
1q
3,即8q
3=1,
∴q=

,
则S
6=
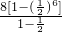
=
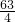
.
故答案为:
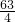
点评:此题考查了等比数列的性质,通项公式,以及求和公式,利用等比数列的性质得出a
2a
3=a
1a
4是解本题的关键.
