
【题目】设函数![]() .
.
(1)若不等式![]() 对任意的
对任意的![]() ,
,![]() 都成立,求实数m的取值范围;
都成立,求实数m的取值范围;
(2)关于x的方程![]() 在
在![]() 上有且只有一个解,求实数k的取值范围.
上有且只有一个解,求实数k的取值范围.
参考数据:![]() .
.
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】甲袋中装有3个白球和5个黑球,乙袋中装有4个白球和6个黑球,现从甲袋中随机取出一个球放入乙袋中,充分混合后,再从乙袋中随机取出一个球放回甲袋中,则甲袋中白球没有减少的概率为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点在抛物线
的左焦点在抛物线![]() 的准线上,且椭圆的短轴长为2,
的准线上,且椭圆的短轴长为2,![]() 分别为椭圆的左,右焦点,
分别为椭圆的左,右焦点,![]() 分别为椭圆的左,右顶点,设点
分别为椭圆的左,右顶点,设点![]() 在第一象限,且
在第一象限,且![]() 轴,连接
轴,连接![]() 交椭圆于点
交椭圆于点![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若三角形![]() 的面积等于四边形
的面积等于四边形![]() 的面积,求
的面积,求![]() 的值;
的值;
(Ⅲ)设点![]() 为
为![]() 的中点,射线
的中点,射线![]() (
(![]() 为原点)与椭圆交于点
为原点)与椭圆交于点![]() ,满足
,满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)求函数![]() 的单调递减区间;
的单调递减区间;
(2)若![]() ,对于给定实数
,对于给定实数![]() ,总存在实数
,总存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 恰有3个不同的实数根.
恰有3个不同的实数根.
(i)求实数![]() 的取值范围;
的取值范围;
(ii)记![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
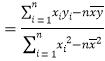 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() .
.
(1)若数列![]() 的首项为
的首项为![]() ,其中
,其中![]() ,且
,且![]() ,
,![]() ,
,![]() 构成公比小于0的等比数列,求
构成公比小于0的等比数列,求![]() 的值;
的值;
(2)若![]() 是公差为d(d>0)的等差数列
是公差为d(d>0)的等差数列![]() 的前n项和,求
的前n项和,求![]() 的值;
的值;
(3)若![]() ,
,![]() ,且数列
,且数列![]() 单调递增,数列
单调递增,数列![]() 单调递减,求数列
单调递减,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,且经过点
的长轴长为4,且经过点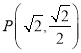 .
.
(1)求椭圆的方程;
(2)直线![]() 的斜率为
的斜率为![]() ,且与椭圆相交于
,且与椭圆相交于![]() ,
,![]() 两点(异于点
两点(异于点![]() ),过
),过![]() 作
作![]() 的角平分线交椭圆于另一点
的角平分线交椭圆于另一点![]() .
.
(i)证明:直线![]() 与坐标轴平行;
与坐标轴平行;
(ii)当![]() 时,求四边形
时,求四边形![]() 的面积
的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com