
【题目】在四棱锥P﹣ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形.AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.
(Ⅰ)求证:BE∥平面APD;
(Ⅱ)求证:BC⊥平面PBD.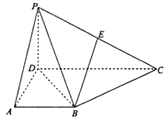
【答案】证明:(Ⅰ)取PD的中点F,连结EF,AF,因为E为PC中点, ∴EF∥CD,且 ![]() ,在梯形ABCD中,AB∥CD,AB=1,
,在梯形ABCD中,AB∥CD,AB=1,
∴EF∥AB,EF=AB,
四边形ABEF为平行四边形,∴BE∥AF,BE平面PAD,AF平面PAD,
∴BE∥平面PAD
(Ⅱ)平面PCD⊥平面ABCD,PD⊥CD,∴PD⊥平面ABCD,∴PD⊥AD
在直角梯形ABCD中, ![]() ,
,
∴∠CBD=90°,即DB⊥BC.
又由PD⊥平面ABCD,可得PD⊥BC,
又PD∩BD=D,∴BC⊥平面PBD.
【解析】
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面垂直的判定的理解,了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增,若实数a满足f(lga)+f(lg ![]() )≤2f(1),则a的取值范围是( )
)≤2f(1),则a的取值范围是( )
A.(﹣∞,10]
B.[ ![]() ,10]
,10]
C.(0,10]
D.[ ![]() ,1]
,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,BC=DC=AB=AD= ![]() ,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P﹣QCO体积的最大值为 .
,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P﹣QCO体积的最大值为 . 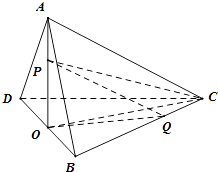
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D为AC的中点,∠ABC=90°,AA1=AB=2,BC=3. 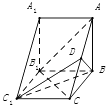
(1)求证:AB1∥平面BC1D;
(2)求三棱锥D﹣BC1C的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验。甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在![]() 区间内(满分100分),并绘制频率分布直方图如右图,两个班人数均为60人,成绩80分及以上为优良。
区间内(满分100分),并绘制频率分布直方图如右图,两个班人数均为60人,成绩80分及以上为优良。

根据以上信息填好下列![]() 联表,并判断出有多大的把握认为学生成绩优良与班级有关?
联表,并判断出有多大的把握认为学生成绩优良与班级有关?

(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选3人来作书面发言,求发言人至少有2人来自甲班的概率。
(以下临界值及公式仅供参考

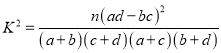 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(1,1),并与直线l1:x﹣y+3=0和l2:2x+y﹣6=0分别交于点A、B,若线段AB被点P平分. 求:
(1)直线l的方程;
(2)以O为圆心且被l截得的弦长为 ![]() 的圆的方程.
的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com