
设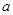 为常数,已知函数
为常数,已知函数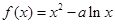 在区间
在区间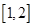 上是增函数,
上是增函数,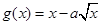 在区间
在区间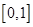 上是减函数.
上是减函数.
(1)设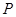 为函数
为函数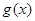 的图像上任意一点,求点
的图像上任意一点,求点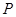 到直线
到直线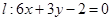 的距离的最小值;
的距离的最小值;
(2)若对任意的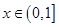 且
且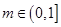 ,
,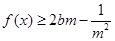 恒成立,求实数
恒成立,求实数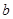 的取值范围.
的取值范围.
(Ⅰ)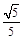 .(Ⅱ)
.(Ⅱ)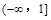 .
.
【解析】
试题分析:(Ⅰ)∵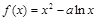 在区间
在区间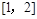 上是增函数,
上是增函数,
∴当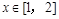 时,
时,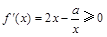 恒成立,即
恒成立,即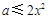 恒成立,所以
恒成立,所以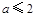 .
.
又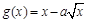 在区间
在区间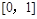 上是减函数,
上是减函数,
故当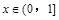 时,
时,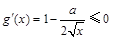 恒成立,即
恒成立,即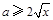 恒成立,所以
恒成立,所以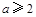 .
.
综上,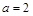 .
.
由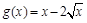 ,得
,得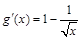 ,
,
令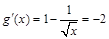 ,则
,则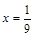 ,而
,而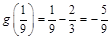 ,
,
所以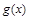 的图象上
的图象上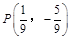 处的切线与直线
处的切线与直线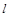 平行,
平行,
所以所求距离的最小值为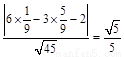 . (6分)
. (6分)
(Ⅱ)因为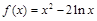 ,则
,则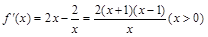 ,
,
因为当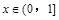 时,
时,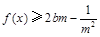 恒成立,所以
恒成立,所以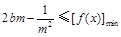 ,
,
因为当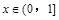 时,
时,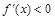 ,所以
,所以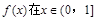 上是减函数,
上是减函数,
从而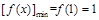 ,
,
所以当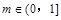 时,
时,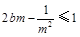 ,即
,即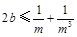 恒成立,所以
恒成立,所以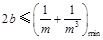 .
.
因为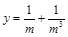 在
在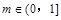 上是减函数,所以
上是减函数,所以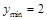 ,
,
从而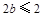 ,即
,即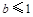 ,
,
故实数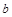 的取值范围是
的取值范围是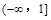 . (12分)
. (12分)
考点:本题考查了导数运用
点评:近几年新课标高考对于函数与导数这一综合问题的命制,一般以有理函数与半超越(指数、对数)函数的组合复合且含有参量的函数为背景载体,解题时要注意对数式对函数定义域的隐蔽,这类问题重点考查函数单调性、导数运算、不等式方程的求解等基本知识,注重数学思想(分类与整合、数与形的结合)方法(分析法、综合法、反证法)的运用.把数学运算的“力量”与数学思维的“技巧”完美结合


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
设a为实常数,已知函数![]() 在区间[1,2]上是增函数,且
在区间[1,2]上是增函数,且![]() 在区间[0,1]上是
在区间[0,1]上是![]() 减函数.
减函数.
(Ⅰ)求常数![]() 的值;
的值;
(Ⅱ)设点P为函数![]() 图象上任意一点,求点P到直线
图象上任意一点,求点P到直线![]() 距离的最小值.
距离的最小值.
(Ⅲ)若当![]() 且
且![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
设a为实常数,已知函数![]() 在区间[1,2]上是增函数,且
在区间[1,2]上是增函数,且![]() 在区间[0,1]上是减函数。
在区间[0,1]上是减函数。
(Ⅰ)求常数![]() 的值;
的值;
(Ⅱ)设点P为函数![]() 图象上任意一点,求点P到直线
图象上任意一点,求点P到直线![]() 距离的最小值;
距离的最小值;
(Ⅲ)若当![]() 且
且![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2013届四川省成都市高二5月月考数学试卷(解析版) 题型:解答题
设函数 ,
,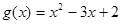 ,其中
,其中 ,a、b为常数,已知曲线
,a、b为常数,已知曲线 在点(2,0)处有相同的切线
在点(2,0)处有相同的切线 。
。
(1)求a、b的值,并写出切线 的方程;
的方程;
(2)求函数 单调区间与极值。
单调区间与极值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com