
【题目】求所有正整数![]() ,使得给定序列
,使得给定序列![]() ,
,![]() ,中的每一项都是平方数。
,中的每一项都是平方数。
【答案】见解析
【解析】
解法1 由已知可得![]() ,
,![]() .
.
则![]() .
.
故![]() .
.
当![]() 时,有
时,有![]() .
.
当![]() 时,有
时,有![]() .
.
当![]() 时,
时,![]() .
.
由于![]() 与
与![]() 互质,则
互质,则![]() 与
与![]() 是一组本原勾股数.
是一组本原勾股数.
因此,存在互质的正整数![]() ,且
,且![]() ,
,
使得(1)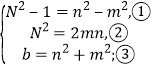
(2)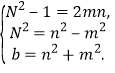
第(1)种情形中,由式①、②得![]() . ④
. ④
由上式知![]() 为奇数,则
为奇数,则![]() 为偶数,
为偶数,![]() 为奇数.
为奇数.
于是,由式②及![]() ,知
,知![]() . ⑤
. ⑤
再利用式④得![]() .
.
则![]() , ⑥
, ⑥
其中,![]() 是相邻的两个整数.
是相邻的两个整数.
由于它们互质,则![]() .
.
于是,![]() .
.
若![]() ,则
,则![]() .
.
此式具有![]() 的形式,已证明它没有满足
的形式,已证明它没有满足![]() 的整数解,故
的整数解,故![]() ,矛盾.
,矛盾.
若![]() ,则
,则![]() .
.
此式具有![]() 的形式,也已证明它没有满足
的形式,也已证明它没有满足![]() 的整数解,故
的整数解,故![]() .
.
于是,![]() .
.
由式④得![]() .
.
由式②知![]() ,从而,
,从而,![]() .
.
第(2)种情形下,没有满足条件的正整数解.
综上,找到了关于![]() 的所有选择
的所有选择
![]() .
.
当![]() 时,得到一个各项均为平方数的周期序列:4,4,0,4,4,0,….
时,得到一个各项均为平方数的周期序列:4,4,0,4,4,0,….
当![]() 时,得到一个各项均为平方数4的常数序列:4,4,4,4,….
时,得到一个各项均为平方数4的常数序列:4,4,4,4,….
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
……
由此可猜测此序列是斐波那契数列中奇数项的平方的4倍,即
![]() .
.
如果![]() 是斐波那契数列,易知
是斐波那契数列,易知![]() 及
及![]() ,
,
故![]() 为平方数.
为平方数.
因此,![]() ,
,
即![]() 为平方数.
为平方数.
这说明![]() 符合题设要求.
符合题设要求.
综上,所有![]() 的取值为1,3,9.
的取值为1,3,9.
解法2 由![]() ,
,![]() ,
,
得![]() .
.
于是,![]() 是偶数,又是平方数.
是偶数,又是平方数.
故可设![]() .
.
从而,![]() .
.
则![]() .
.
故![]() ,
,
![]() .
.
由![]() 是平方数,可设
是平方数,可设![]() . ①
. ①
当![]() 时,
时,![]() .
.
此时,![]() ,
,
![]() ,
,
![]() .
.
从而,数列![]() 的周期数列:
的周期数列:
4,4,0,4,4,0,….
因此,![]() 满足条件.
满足条件.
当![]() 时,
时,![]() .
.
从而,数列![]() 为常数数列; 4,4,4,….
为常数数列; 4,4,4,….
因此,![]() 满足条件.
满足条件.
当![]() 时,有式①知
时,有式①知![]() , ②
, ②
![]()
![]()
![]() .
.
故![]()
![]() .
.
从而,![]() ,即式②等号成立.
,即式②等号成立.
于是![]() .此时,
.此时,![]() .
.
以下同解法1.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 的展开式中第5项与第7项的二项数系数相等,且展开式的各项系数之和为1024,则下列说法正确的是( )
的展开式中第5项与第7项的二项数系数相等,且展开式的各项系数之和为1024,则下列说法正确的是( )
A.展开式中奇数项的二项式系数和为256
B.展开式中第6项的系数最大
C.展开式中存在常数项
D.展开式中含![]() 项的系数为45
项的系数为45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆的焦点且与长轴垂直的弦长为1.
,过椭圆的焦点且与长轴垂直的弦长为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上第一象限内一动点,A,B分别为椭圆的左顶点和下顶点,直线MB与x轴交于点C,直线MA与y轴交于点D,求证:四边形ABCD的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水果经销商为了对一批刚上市水果进行合理定价,将该水果按事先拟定的价格进行试销,得到一组销售数据,如表所示:
试销单价 | 16 | 17 | 18 | 19 | 20 |
日销售量 | 168 | 146 | 120 | 90 | 56 |
(1)已知变量![]() 具有线性相关关系,求该水果日销售量
具有线性相关关系,求该水果日销售量![]() (公斤)关于试销单价
(公斤)关于试销单价![]() (元/公斤)的线性回归方程,并据此分析销售单价
(元/公斤)的线性回归方程,并据此分析销售单价![]() 时,日销售量的变化情况;
时,日销售量的变化情况;
(2)若该水果进价为每公斤![]() 元,预计在今后的销售中,日销售量和售价仍然服从(1)中的线性相关关系,该水果经销商如果想获得最大的日销售利润,此水果的售价
元,预计在今后的销售中,日销售量和售价仍然服从(1)中的线性相关关系,该水果经销商如果想获得最大的日销售利润,此水果的售价![]()
![]() 应定为多少元?
应定为多少元?
(参考数据及公式:![]() ,
,![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,
,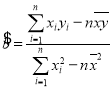 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形ABCD外切于![]() ,△ACB的内切圆
,△ACB的内切圆![]() 与边AB、BC的切点分别为P、Q,,△ACD的内切圆
与边AB、BC的切点分别为P、Q,,△ACD的内切圆![]() 与边CD、DA的切点分别为R、S. 求证:三条直线PQ、RS、AC共点或平行.
与边CD、DA的切点分别为R、S. 求证:三条直线PQ、RS、AC共点或平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(ax+b)-x2-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4.
(Ⅰ)求a,b的值;
(Ⅱ)讨论f(x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上![]() 至
至![]() 之间到某公交站搭乘公交车去上学,已知在这段时间内,共有
之间到某公交站搭乘公交车去上学,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为
班公交车到达该站,到站的时间分别为![]() ,
,![]() ,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com